Brojevni sistem je sistematičan način predstavljanja brojeva pomoću simboličkih znakova u kome se koristi osnovna vrednost kako bi se brojevi grupisali u sažeti oblik. Najčešći brojevni sistem je decimalni(dekadni), čija je osnovna vrednost 10, a grupa simboličkih znakova 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Međutim, postoje i drugi brojevni sistemi koji se mogu efikasnije koristiti u određene svrhe. Na primer, pošto računari koriste Bulovu logiku za obavljanje operacija, oni koriste binarni brojevni sistem, čija je osnovna vrednost 2.
Binarni brojevni sistem (BIN) je brojčani sistem u kome se zapis sastoji samo od cifara 0 i 1. Ovo je pozicioni brojčani sistem, sa osnovom 2. Svaki broj se može predstaviti kao zbir eksponenata dvojke.
Svaki broj X iz Binarnog brojnog sistema moze da se predstavi kao:
x=b_R2^R+b_{R-1}2^{R-1}+...+b_12^1+b_02^0+b_{-1} 2^{-1}+...+b_{-p}2^{-p}
Konverzija iz dekadnog (decimalnog) u binarni zasniva se na deljenju. Logično je da se suprotna transformacija, binarnog u dekadni, zasniva na množenju (binarna cifra se množi stepenom osnove, i onda dodaje na sumu).
Primeri konverzije
Prikazaćemo kako da prevedemo broj 68 iz dekadnog u binarni broj:
68:2=34 ostatak: 0
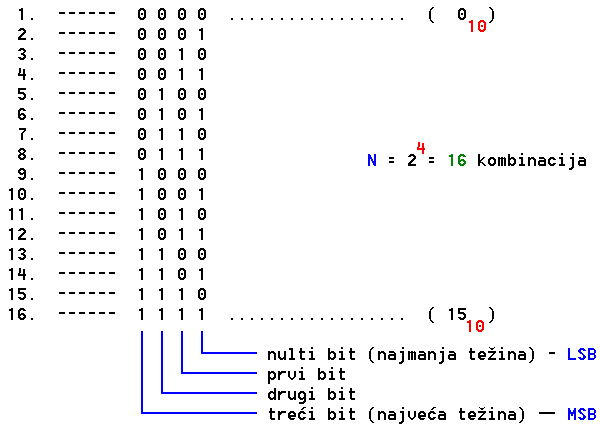
Napomena: Prvi dobijeni ostatak, u ovom slučaju 0, biće cifra najmanje težine binarnog broja (LSB) i upisujemo je na poziciju najmanje težine.
34:2=17 ostatak: 0
17:2=8 ostatak: 1
8:2=4 ostatak: 0
4:2=2 ostatak: 0
2:2=1 ostatak: 0
1:2=0 ostatak: 1
Postupak se završava kada se u deljenju dođe do nule (1:2=0, ostatak 1). Dobijeni binarni broj je: 1000100
(68)_{10}=(1000100)_2
Postupak prevođenja razlomljenog (broj sa decimalama) broja je sličan prevođenju celog broja, osim što se umesto deljenja, vrši množenje sa 2 (množenje sa osnovom). Sada se ne gleda ostatak pri deljenju već da li se pri množenju dvojkom, pojavila jedinica ispred zareza (u celom delu broja), i ako se pojavila – ona se upisuje u binarni broj. Nakon upisivanja jedinice u dobijeni binarni broj, nadalje se množi samo razlomljni deo broja.
Prikazaćemo kako da prevedemo dekadni 0,84375 u binarni broj:
0,84375·2=1,6875
Prilikom množenja dvojkom, pojavila se jedinica u celobrojnom delu. To je prva cifra prevedenog binarnog broja koja stoji iza decimalnog zareza.
0,6875·2=1,375
0,375·2=0,75
0,75·2=1,5
0,5·2=1,0
0,0
Prevođenje prekidamo kada dekani broj postane 0.
Dobijeni prevedeni binarni broj je sada: 0,11011
Binarni brojevni sistem (BIN) je svoju glavnu primenu našao u računarstvu. Velika većina modernih računara koristi binarnu logiku tj. podatke zapisuje i interpretira u obliku nula i jedinica. Zbog jednostavnosti primene u elektronskim kolima, binarni sistem koriste praktično svi moderni računari.
[…] https://www.automatika.rs/baza-znanja/tutorijali/kako-pretvoriti-decimalni-u-binarni-broj.html […]
Zar nisu u primeru ispomerane vrednosti za jedan? Nula bi trebalo da bude 0000, a 15 1111, a 16 10100.