Šta je fuzzy logika? Da bi odgovorili na ovo pitanje, uporedićemo ovaj pristup sa konvencijalnom logikom. Osnove klasične logike je učvrstio još u antičkoj Grčkoj poznati filozof Aristotel. Ova logika se zasniva na jasnim i precizno utvđenim pravilima, a počiva na teoriji skupova. Neki element može da pripada nekom skupu ili da ne pripada. Skupovi imaju jasno određene granice.
Tako su ovakvi skupovi, pa sa njima i logika, nazvani engleskom reči crisp, koja ima značenje – jasan, bistar. Fuzzy je engleska reč koja bi mogla da se prevede kao maglovito, nejasno, mutno. U fuzzy logici nije precizno definisana pripadnost jednog elementa određenom skupu, već se pripadnost meri u,recimo, procentima. Ove mere pripadnosti, skalirane, mogu da uzimaju vrijednosti od 0 do1.
Fuzzy logika kao koncept je puno prirodniji nego što se to na prvi momenat misli. Naime, postoje situacije u kojima nije moguće znanje o sistemu reprezentovati na apsolutno precizan način. Čak je više situacija u kojima moramo da koristimo neprecizne konstatacije. Na primer “Marko je visok čovek.”, “Onaj automobil se približava jako velikom brzinom.” su neprecizne rečenice, a ipak ih svakodnevno koristimo. Da bismo bili u stanju reprezentovati znanje o ovakvim sistemima (a ima ih jako puno) moramo da se odreknemo klasične (binarne) logike u kojoj je nešto ili tačno ili netačno (crno ili belo) i da koristimo fuzzy logiku („sve je nijansa sive boje“).
Primer
Kao primer uzećemo dane u nedelji i napraviti dva skupa. Skup radnih dana i skup vikenda. U crisp logici bi se u skupu radnih dana našli: ponedeljak, utorak, sreda, četvrtak i petak, a u skupu vikend dana: subota i nedelja. Pripadnost elementa nekom skupu bi se izrazila brojem 1, a nepripadanje brojem 0. Međutim u fuzzy zaključivanju bi situacija bila nešto drugačija. Petak, kao dan koji je delom radni dan, a delom početak vikenda bio bi negde na granici ova dva skupa tj. njegova pripadnost prvom, skupu radnih dana bi se izražavala, recimo brojem 0,75 dok bi pripadnost drugom, skupu vikend dana bila cifra 0,25. Slično bi bilo i za nedelju kao dan koji jeste vikend, ali ne sasvim, cijelim svojim trajanjem, jer ipak se nedelja uveče doživljava kao priprema za novu radnu nedelju odnosno mnogi ljudi će ga okarakterisati kao ne sasvim vikend dan, jer posle njega dolazi ponedeljak.
Vidimo da je ova logika jako bliska ljudskoj percepciji o mnogim stvarima u životu. Mnoge slične situacije koje nisu jasno razdvojene, koje su mešavina više stvari su svakodnevno prisutne oko nas. Da li je desetogodišnjak koji sebe smatra visokim stvarno i visok? Ovde “da – ne” (tačno – netačno) logika više nije upotrebljiva. U fuzzy logici istinitost svakog tvrđenja se meri u procentima.
Fuzzy skupovi
Fuzzy skupovi su osnovni elementi kojima opisujemo nepreciznost. Naime, diskretan skup (klasičan) sadrži elemente sa istim svojstvima (skup jabuka, skup krušaka, skup celih brojeva itd.), dok fuzzy skupovi sadrže elemente sa sličnim svojstvima (skup visokih ljudi, skup niskih ljudi, skup brzih automobila itd.).
U diskretnim skupovima element ili pripada ili ne pripada određenom skupu, ako to predstavimo matematički kažemo da je stepen pripadnosti skupu 1 (ako pripada) ili 0 (ako ne pripada). Sa druge strane elementi u fuzzy skupovima mogu delimično da pripadaju, matematički to možemo da predstavimo na sledeći način 1 (100% pripada), 0 (uopšte ne pripada skupu), 0.7 (70% pripada skupu). Ovim pristupom možemo preciznije da reprezentujemo neprecizne iskaze.
Primena fuzzy sistema
U nastavku će biti prikazan primer upotrebe fuzzy logike u rešavanju problema automatskog upravljanja realnim sistemom. Kao realni sistem posmatraćemo sistem za upravljanje kočenjem automobila, koji na osnovu brzine automobila i rastojanja do susednog vozila određuje potrebnu silu kočenja, kako bi se izbegao sudar.
Prvi korak u rešavanju ovog problema je podela skupa mogućih vrednosti stanja u nekoliko kategorija. Na primer, brzinu automobila (0-200 km/h) delimo u dve kategorije: mala_brzina i velika_brzina, a rastojanje do susednog vozila (0,5 – 200 m) delimo na veliko i malo rastojanje. Ovim su definisane ulazne veličine. Kako bismo definisali izlazne moramo podeliti skup mogućih akcija na nekoliko skupova ili kategorija. Silu kočenja (0-1000 N) delimo u tri fuzzy skupa: slabo_kočenje, srednje_kočenje i veliko_kočenje.
Pošto smo definisali fuzzy skupove, sada je potrebno, na osnovu iskustava, napisati fuzzy pravila ili fuzzy relacije na osnovu kojih će se izvoditi zaključak. Za konkretan sučaj fuzzy pravila bi mogla da izgledaju ovako: ako je mala_brzina i veliko_rastojanje treba aktivirati slabo_kočenje; ako je velika_brzina i malo_rastojanje treba aktivirati veliko_kočenje. Na kraju, potrebno je definisati funkcije pripadnosti koje opisuju fuzzy skupove (posebno za svaku veličinu).
Fuzzy logika i upravljanje
Do danas su razvijane mnoge tehnike projektovanja kontrolera koje bi trebalo da omoguće jasnu metodologiju za ostvarivanje željenih performansi i specifikacija koje kontroler treba da ispuni. Ove tehnike se razlikuju i u pristupu, pa se tako izdvajaju različiti kontroleri: linearni, robusni, nelinearni, adaptivni, zasnovani na prostoru stanja itd. Fuzzy upravljanje obezbeđuje formalnu metodologiju za predstavljanje, manipulaciju i implementaciju ljudskog heurističkog predznanja o tome kako kontrolisati jedan, određeni sistem.
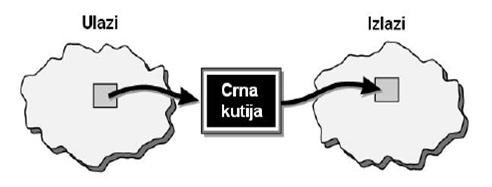Slika 1. Fuzzy regulator.
Jedan relativno nov pristup upravljanja je primena fazi regulatora (slika 1). Suština je u formiraju programskog koda koji implementira znanje čoveka eksperta o nekim procesima. Ovo ne isključuje razvoj modela procesa jer nam je ovaj model u svakom slučaju potreban za detaljnu simulaciju ponašanja kontrolera u cilju ispitivanja zadovoljenja performansi, stabilnosti sistema kao i za ispitivanje krajnjih ograničenja samog dizajna. Cilj fuzzy pristupa je da, umesto da jezikom matematike, pokuša da što bolje reši problem upravljanja sistemom i omogući implementaciju inženjerskog iskustva o procesu u sam algoritam kontrolera. Na slici 2, prikazana je struktura FLC-a (Fuzzy Logic Controler), tj. kontrolera u koji je implementiran algoritam upravljanja baziran na fuzzy logici.
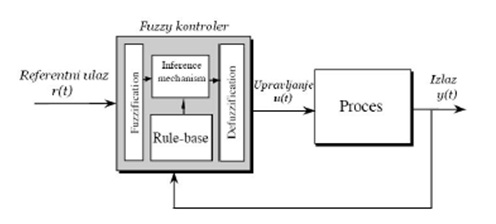Slika 2. Struktura fuzzy kontrolera.
Kako projektovati fuzzy kontroler
U osnovi, na fuzzy kontroler treba gledati kao na veštačkog donosioca odluke koji radi u sistemu sa zatvorenom spregom u realnom vremenu. On „sakuplja“ podatke izlaza procesa, upoređuje ih sa referencom i onda na način svojstven fuzzy logici „odlučuje“ šta u tom trenutku treba da bude ulaz procesa, i to tako da se zadovolje željene performanse i zadati ciljevi specifikacije. Da bi projektovali jedan fuzzy kontroler, potrebno nam je pre svega određeno predznanje o ponašanju procesa.
Heurističke informacije o tome kako najbolje upravljati nekim procesom mogu da se prikupe na dva načina. Informacije najčešće dobijamo od operatera koji ima dovoljno iskustvenih podataka o tome kako na najbolji način upravljati procesom. Ređe zaključke o upravljenju procesa donose specijalno angažovani inženjeri koji, shvatajući dinamiku procesa, mogu da odrede pravila po kojima bi se procesom moglo upravljati. Ova pravila nam govore kakav bi trebao da bude ulaz procesa ako se njegov izlaz ponaša na takav i takav način.
Tekst je preuzet iz seminarskog rad ”Fuzzy logika” autora Vrtunić Mileta. Dalja objašnjenja pojmova korišćenih u ovom tekstu možete naći u pomenutom radu.
