Z-transformacija je diskretni ekvivalent Laplaceove transformacije. Međutim, dok je Laplaceova transformacija otkrivena još krajem 18. veka (1799. godine), Z-transformacija je uvedena sredinom 20. veka (početkom 1950. godine), a svoju primenu u teoriji diskretnih signala i sistema našla je krajem 50-tih i početkom 60-tih godina prošlog veka (radovi Ragazzinija, Zadeha, Jury-ja, Franklina i Tsypkina).
Vremenski diskretan signal obično se dobija uniformnim odabiranjem (odmeravanjem ili semplovanjem) kontinualnog signala svakih T sekundi, mada postoje i slučajevi gde je signal po svojoj prirodi vremenski diskretan i predstavljen samo preko svojih odbiraka (odmeraka ili semplova) f[k]. Zbog jednostavnosti označavanja, čak i kad se predstavlja vremenski-diskretan signal f(kT) , koji je generisan semplovanjem vremenski kontinualnog signala f(t)sa periodom semplovanja (odabiranja, odmeravanja) T , uobičajeno je da se T ne označava, te da se f(kT) predstavi takođe sa f [k], gde je k indeks vremena koji odgovara trenutku odabiranja (semplovanja ili diskretizacije) tk.
Z-transformacija se može uvesti polazeći od Laplaceove transformacije na sledeći jednostavan način. Pošto je Laplaceova transformacija kontinualnog signala definisana preko integrala
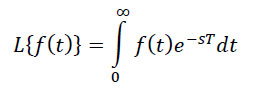
uvodeći smenu z=esT, dobija se sledeći izraz:
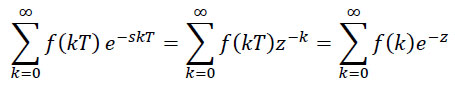
Ovako definisana suma, čije članove predstavljaju odbirci diskretnog signala f[k] pomnoženi sa kompleksnom varijablom z dignutim na stepen (− k), tj. pomnoženi sa z-k, predstavlja funkciju kompleksne varijable z i naziva se unilateralna (jednostrana) Z -transformacija diskretnog signala f[k]. Dakle, jednostrana (unilateralna) transformacija diskretnog signala f[k] definisana je sumom:
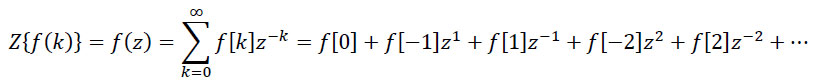
- Unilateralnu (jednostranu)
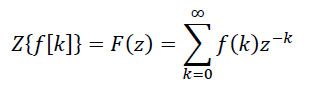
- Bilateralnu (dvostranu)
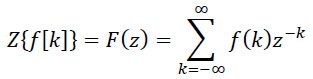
- Geofizičku
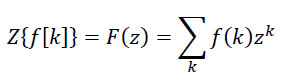
Inverzna Z – transformacija
Postoji nekoliko različitih načina kako se iz funkcije X(z) mogu rekonstruisati vrednosti odbiraka x[k]. Prvi od njih je, svakako teorijski vrlo značajan, međutim prektično često nepodesan i komplikovan a zasniva se na Cauchy-jevom integralu i teoriji kompleksne promenljive.
Mnogo jednostavniji način određivanja odbiraka na osnovu Z-transformacije se sastoji u razvoju funkcije X(z) u petencijalni red. Ako funkciju X(z) napišemo u sledećem obliku:
F(z)=B(z)/A(z)
deljenjem polinoma B(z) polinomom A(z) dobija se potencijalni red oblika:
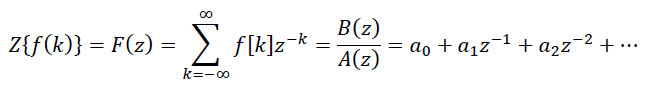
gde se upoređivanjem koeficijenata redova na levoj i desnoj strani dolazi do zaključka da koeficijen razvoja koji stoji uz član zk zapravo predstavlja vrednost odbirka x[-k].
Osobine unilateralne Z-transformacije:
- Linearnost
- Pomeranje signala u vremenu udesno
- Pomeranje signala u vremenu ulevo
- Množenje signala sa vremenskim faktorom
- Množenje signala sa eksponencijalnim faktorom ili skaliranje Z kompleksne učestanosti
- Modulacija signala
- Konvolucija
- Granične teoreme Z-transformacije
Osobine bilateralne Z-transformacije:
- Linearnost
- Pomeranje u vremenu
- Modulacija
- Inverzija vremena
- Konvolucija signala
Literatura:
- Sistemi i signali, prateći materijal za vežbe, Odsek za Signale i sisteme, ETF Beogtad
- Signali i sistemi – Branko Kovačević, Željko Đurović, Srđan Stanković
Dalja objašnjenja pojmova korišćenih u ovom tekstu, izvođenja i dokaze osobina Z-transformacije možete naći u pomenutim knjigama.
