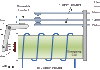
Audiopojačavači klase D se razlikuju od ostalih klasa jer rade na potpuno drugačijem principu. Ovu vrstu pojačavača nazivaju i “digitalni” pojačavači, zbog samog oblika signala, iako se pod digitalnim pojačavačima smatraju sklopovi koji pojačavaju digitalni signal. Pojačavači klase D se baziraju na široko-impulsnoj modulaciji. Trajanje poluperioda pravougaonog signala zavisi o vrednosti analognog nisko-frekventnog signala. Na izlazu iz modulatora se nalazi pravougaoni signal sa samo dve vrednosti.
Impulsno širinska modulacija(PWM)
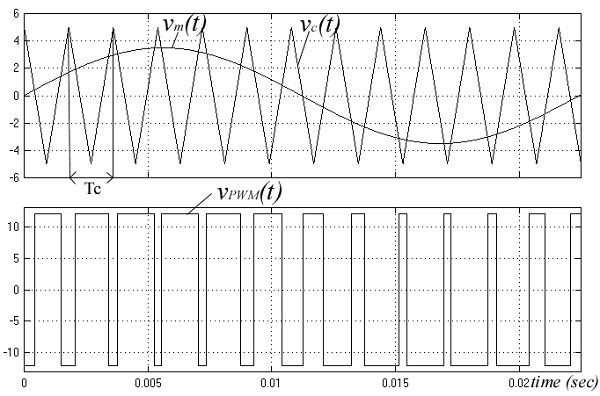
Impulsno širinska modulacija ili PWM nastaje poredjenjem dva signala i to nosećeg vc(t) i modulišućeg Vm(t). Noseći signal je testerasti, a modulišući je audio signal . Kada je amplituda modulišućeg signala Vm veća od amplitude nosećeg signala Vc, na izlazu PWM-a dobijamo logičku 1, a u suprotnom logičku 0. To poredjenje možemo predstaviti funkcijom vpwm(t), datom u uopštenom slučaju:
U našem buduće posmatranom slučaju, gde Vo predstavlja izlazni napon PWM modulatora vpwm(t) možemo iskazati kao:
Za modulišući signal vm(t)=Vmsinωm t i noseći testerasti signal kojeg možemo predstaviti sa:
(i =1,2,3…predstavlja odgovarajuci i-ti interval nosećeg signala u trajanju od Tc/2), na izlazu PWM-a dobijamo povorku pravougaonih impulsa čija se širina menja u skladu sa funkcijom vpwm(t)(slika 1.).
Slika 1. Osnovni princip rada PWM modulatora
Kružna učestanost modulišućeg signala data je sa:
gde je fm učestanost modulišućeg signala. SaTc je predstavljena perioda nosećeg signala, pa je stoga:
Kod PWM-a možemo definisati dva bitna parametra modulacije:
1. Odnos noseće učestanost trouglastog signala i modulišućeg, dat je sa F=fc/fm. Od vrednosti ovog parametra zavisi izgled frekventnog spektra, odnosno položaj učestanosti viših harmonika u odnosu na osnovnu učestanost. Kod praktično realizovanih PWM modulatora ovaj broj se kreće od 10 pa naviše.
2. Indeks modulacije M predstavlja odnos amplituda modulišućeg signala i nosećeg, M=Vm/Vc. M utiče na odnos širina impulsa na izlazu PWM-a, odnosno što je M blize vrednosti 1 to je odnos širina impulsa pri minimalnoj i maksimalnoj vrednosti ulaznog signala veći. Mogu se posmatrati tri opsega vrednosti indeksa M: M>1; M=1 i M<1. Od ove tri vrednosti najčesće se koristi slučaj kada je M≤1.
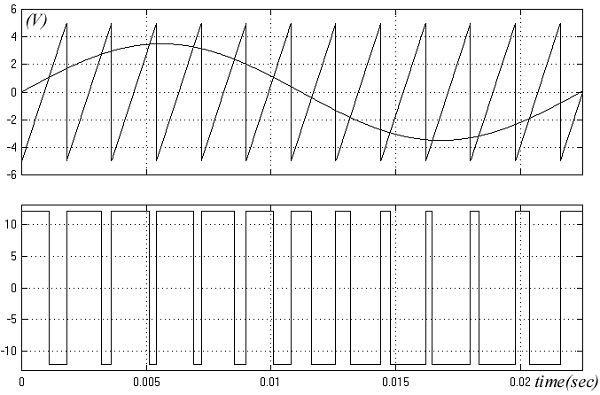
Sam PWM modulator je jednostavne kostrukcije, lako se može realizovati pomoću odgovarajućeg generatora testerastog napona i komparatora. Uloga komparatora je da uporedi vrednosti ulaznih signala i na svome izlazu generiše funkciju vpwm(t). Pored testerastog signala sa slike 3.1a, može se koristiti i drugačiji oblik nosećeg signala prikazanog na slici 2, koji suštinski ne donosi ništa novo.
Slika 2. Alternativni način PWM modulacije
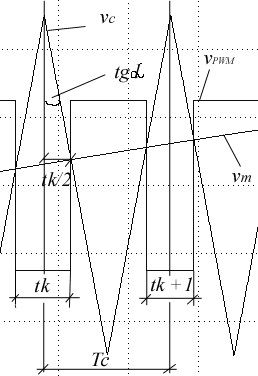
Za povorku pravougaonih impulsa amplitude Vo datih na slikama 1. i 2. možemo pokazati da se srednja vrednost funkcije vpwm(t), menja u skladu sa modulišućim signalom, uz uslov da je parametar F dovoljno velik. Tada se modulišući signal sporo menja u odnosu na noseći (slika 3.) i možemo prihvatiti da je tk≈tk+1.
Slika 3.
Srednja vrednost funkcije vpwm(t) u k-tom intervalu funkcije vm(t), periode Tm data je sa:
Poslednja jednačina proizilazi iz podudarnosti odgovarajućih trouglova, pri čemu je sa vmk obeležena vredost modulišućeg signala u k-tom, posmatranom intervalu.
Na kraju, posle smene, nalazimo srednju vrednost funkcije vpwm(t) u k-tom intervalu:
Za veliku vrednost prametra F, možemo prihvatiti da je Tm≈nxTc, gde je Tm perioda modulišućeg signala. Ako izvršimo sumiranje svih srednjih vrednosti funkcije VPWMsrednjek, u n k-tih intervala trajanja Tc, dobijamo srednju vrednost funkcije vpwm(t) , datu sa:
Iz gore izvedene srednje vrednosti povorke pravougaonih impulsa na izlazu PWM-a, vidimo da se ona menja u ritmu modulišućeg signala. Ako iz te povorke na adekvatan način izdvojimo srednju vrednost (filtriranjem), možemo teoretski ostvariti maksimalnu amplitudu izlaznog signala Vout=Vo, (Vo – amplituda impulsa na izlazu PWM-a) pri maksimalnom indeksu modulacije M=1. Amlituda izlaznog signala, može se menjati promenom indeksa modulacije M, u granicama od 0 do 1 uz pretpostavku da nam je Vo=const. Ovo razmatranje čini suštinu rada pojačavača klase D.
Pojačavač klase D sa otvorenom povratnom spregom
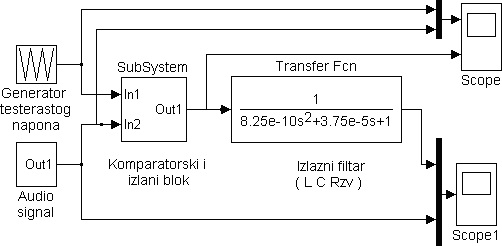
Pojačavač klase D sa otvorenom povratnom spregom možemo predstaviti sistemom prikazanim na slici 4. To je sistem koji predstavlja matematički model pojačavača klase D, pogodanog za analizu uz pomoć programskog paketa “ MatLab”.
Slika 4. Sistem sa otvorenom povratnom spregom
Sam princip rada pojačavača je jednostavan. Na komparator stiže signal sa generatora testerastog napona i audio signal, koji se tu porede. Na izlazu dobijmo impulsno širinsko modulisanu povorku impulsa koji zadovoljavaju funkciju vpwm(t). Ova povorka impulsa sa izlaza komparatora služi kao upravljački signal pobudnog kola polumostnog ili mostnog invertora (slika 5.). Invertor obezbedjuje potrebnu struju potrošaču – zvučniku.
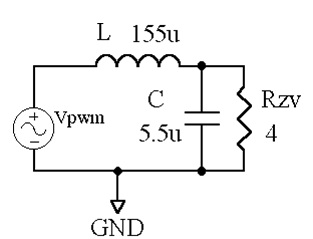
Pre nego što pobudni napon sa izlaza invertora stigne do potrošača, mora proći kroz filtarsko kolo. Ono je dato sa prenosnom funkcijom F(s) LCRzv-filtra sa slike 6. Filtarsko kolo mora biti dovoljno selektivno kako bi se sprečio prolazak viših harmonika sa izlaza invertora. Na taj način, izdvojili smo srednju vrednost PWM signala, koji se menja u skladu sa modulišućim audio signalom.
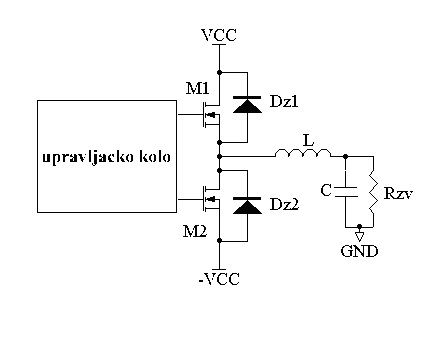
Slika 5. prikazuje funkcionalnu šemu polumostnog invertora koji je ralizovan sa N kanalnim MOSFET tranzistorima. Diode imaju ulogu zaštite mos tranzistora od prenapona, jer su filtar i zvučnik induktivnog karaktera. Na ovaj način deo energije koji se akumuliše u induktivnostima vraćamo napajanju. Kao prekidačke komponente su izabrani mos tranzistori jer jedino oni mogu efikasno raditi na nama potrebnoj prekidačkoj frekvenciji. Sve ostale komercijalno dostupne komponente kao što su IGBT i BJT tranzistori, imaju znatno lošije prekidačke karakteristike u pogledu brzine rada na frekvencijama reda n x 100KHz, koje su ovde zastupljene.
Slika 5.
Na slici 6. prikazano je korišćeno filtarsko kolo, a na slici 7. amplitudska i frekventna karakteristika izlaznog filtra, dobijena simulacijom. Pri simulaciji korišćeni su sledeci parametri:
• Najviša učestanost u spektru audio signala fm=5 kHz,
• Perioda testerastog signala je Tc=0.000013s, => fc=75kHz, odnosno F=fc/fm=15,
• Indeks modulacije M<0.7 pri amplitudi testerastog napona Vc=4V (slika 8.),
• Izlazna amplituda polumostnog invertora Vo=12V,
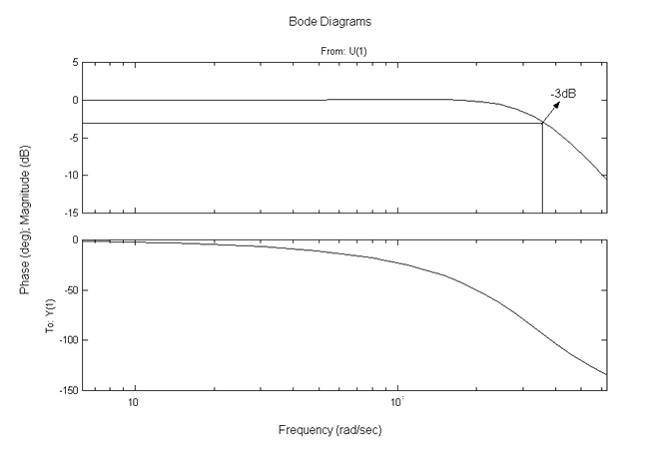
• Slabljnje izlaznog LCRzv-filtra na učestanosti ω0 =2πfo=31400 rad/s
As = -3dB (fo=5kHz).
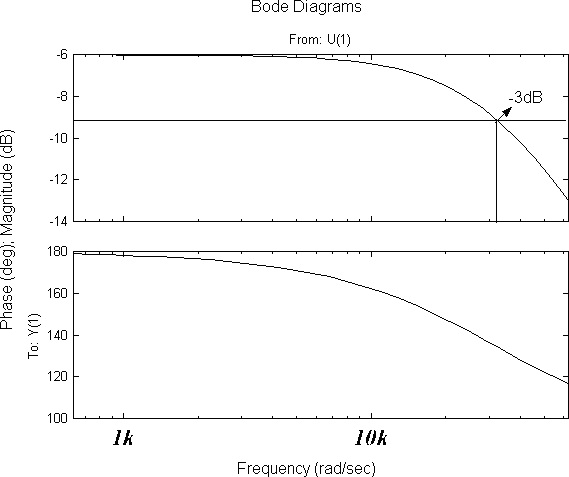
Za navedene parametre nalazimo prenosnu funkciju LCRzv izlaznog filtra , datog na slici 7.:
Koristeći Laplasovu transformaciju i uvodeći smenu jw=s, dobijamo prenosnu funkciju filtarskog kola:
Slika 6. Filtarsko kolo
Slika 7. Bodeov dijagram LCRzv filtarskog kola
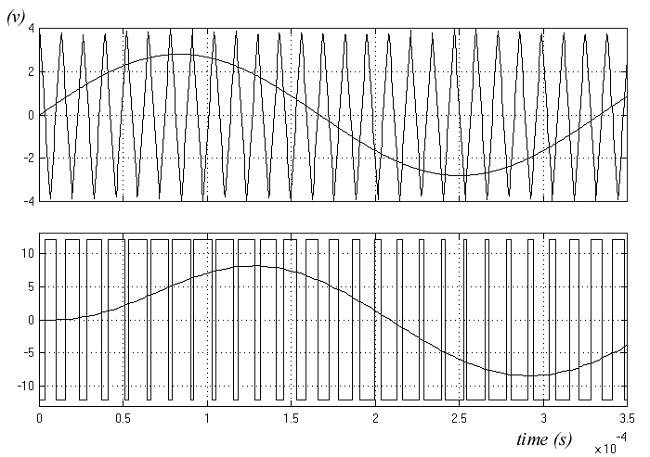
Na slici 8. prikazan je odziv sistema na sinusnu pobudu za M=0.7. Izlazni signal kasni za ulaznim što je posledica kašnjenja koje unosi izlazni filtar i sam PWM modulator. Može se uočiti i prelazni period u trajanju od nekoliko perioda nosećeg signala Tc. Ovo je posledica punjenja kondezatora C po startovanju pojačavača.
Slika 8. Odziv sistema na sinusnu pobudu
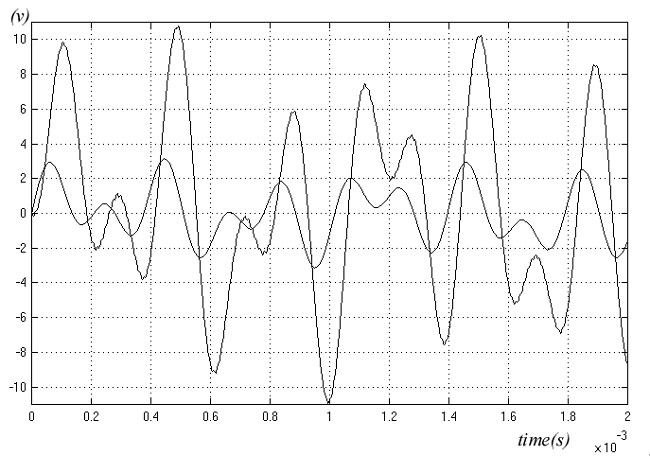
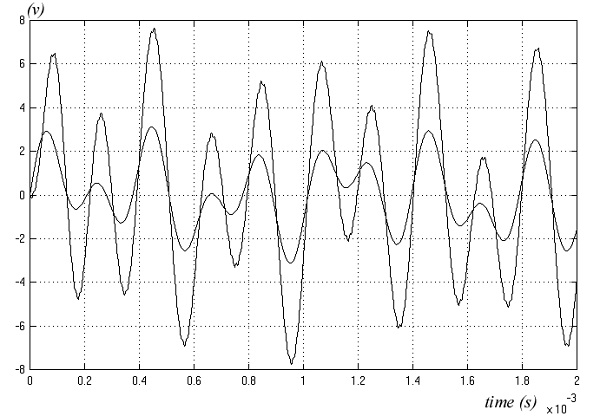
Na slici 9. prikazan je odziv sistema na audio signal, aproksimiranog sa tri različite učestanosti. U maksimumima i minimumima izlaznog signala primetna su izobličenja koja su posledica dva faktora. Prvi uzrok, posledica je potrebe za što većom učestanosti nosećeg testerastog signala, a drugi leži u indeksu modulacije koji je za minimume i maksimume ulaznog signal blizak jedinici.
Slika 9. Odziv sistema na audio signal
Teoretski gledano na izlazu polumostnog invertora, za indeks modulacije M=1 i idealne prekidačke komponete, mogli bi dobiti izlaznu amplitudu jednaku naponu napajanja Vcc. Medjutim, zbog postojanja neke male ali konačne vrednosti otpora kanala mos tranzistora u zasićenju, izlazni napon će sigurno biti manji od napona napajanja, ali ne značajno jer je ta otpornost skoro zanemarljivo mala.
Pojačavač klase D sa zatvorenom povratnom spregom
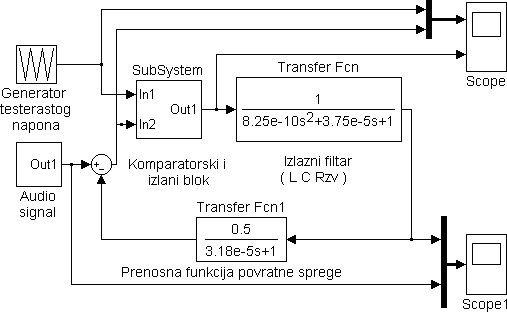
U cilju poboljšavanja karakteristika pojačavača i jednostavnog regulisanja pojačanja uvodimo negativnu povratnu spregu. Pojačavač klase D sa zatvorenom negativnom povratnom reakcijom, možemo predstaviti matematičkim modelom, datim na slici 10.
Slika 10. Matematički model pojačavača klase D sa zatvorenom povratnom spregom
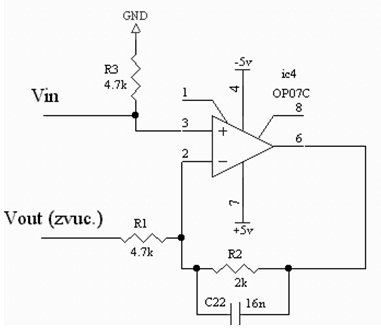
Jedna od mogućih realizacija kola povratne sprege (pojačavača greske) prikazana je na slici 11. Ovakvom konstrukcijom omogućeno je nezavisno menjanje parametra k (slabljenja ili pojačanja) u brojiocu prenosne funkcije R(s), od učestanosti pola (fp= 5kHz). Prenosnu funkciju ovog kola nalazimo iz izraza za naponsko pojačanje invertujućeg pojačavača datog sa: Au=-R2/R1, pri Vin= 0V.
Slika 11. Kolo povratne reakcije
Koristeci Laplasovu transformaciju, odnosno uvodeći smenu jw=s dobijamo prenosnu funkciju kola povratne reakcije:
Simulacijom prenosne funkcije kola povratne sprege, dobijamo “ Bodeove” dijagrame amplitudske i fazne karakteristike, prikazanih na slici 12.
Slika 12. Bodeov dijagram kola povratne sprege
Korišćenjem ovakve povratne sprege onemogućili smo sabiranje viših harmonika sa izlaza pojačavača i ulaznog signala. Sam pojačavač klase D je izrazito nelinearan sklop i u suštini povratna sprega ne moze otkloniti nelinearnost, niti smanjiti amplitude viših harmonika, što je postizano kod pojačavača klase AB, koji su daleko linearniji. Radi ostvarivanja čistijeg signala na izlazu potreban nam je što selektivniji filtar.
Posmatrajući faznu karakteristiku izlaznog filtra sa slike 7. i kola povratne sprege sa slike 12, zaključujemo da fazni stav kružnog pojačanja βA, neće biti potrebnih 180° stepeni duž celog propusnog opsega, već će pri krajevima biti manji (nije uzet u obzir uticaj PWM-a). Medjutim ovu pojavu ne možemo lako eliminisati, što prouzrokuje neravnomerno pojačanje duž propusnog opsega pojačavača. Ako koristimo navedeno kolo povratne reakcije tada nam na ulazu treba sabirač, a ne oduzimač kao što je pokazano na slici 10.
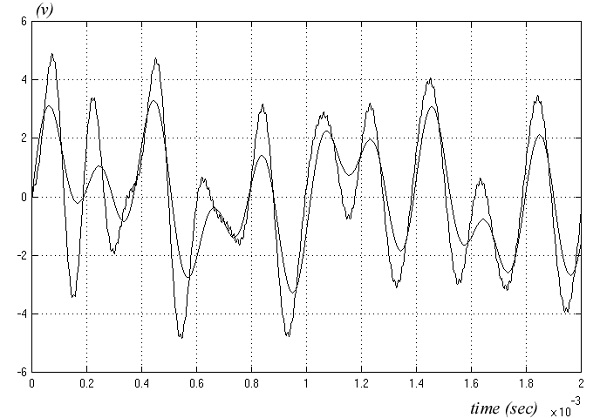
Na slici 11, prikazan je odziv sitema na aproksimirani audio signal. Sada je amplituda izlaznog signala manja u odnosu na sistem sa otvorenom povtatnom spregom. Ovo je posledica vraćanja dela izlaznog signala na ulaz pojačavač. Fazna razlika izmedju ulaznog i izlaznog signala u odnosu na sistem sa otvorenom povratnom spregom (slika 9.), takodje je manja.
Slika 13. Odziv sistema sa z.p.s. na audio signa
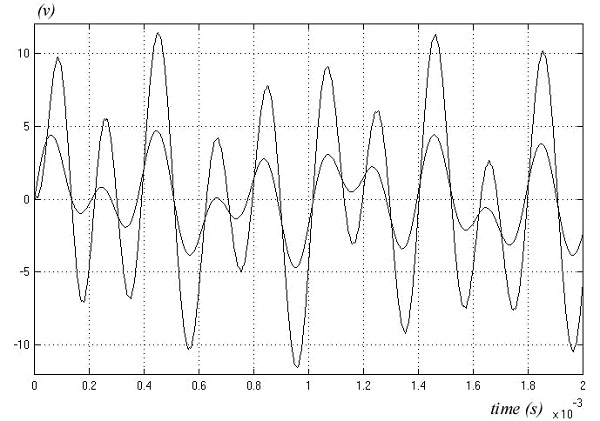
Na slici 14, prikazan je odziv sistema za koeficijent k=1, pri istoj vrednosti pobudnog audio signala. Ukupno pojačanje pojačavača sada je blisko jedinici.
Na slici 15, prikazan je odziv sistema za koeficijen k=0.5, pri čemu radi dobijanja iste vrednosti izlazne amlitude kao kod sistema sa otvorenom povratnom spregom (slike 9.), ulazni audio signal mora biti već amplitude. Ovo je posledica uvođenja negativne reakcije koja je smanjila ukupno naponsko pojačanje Au. Simulacijom u programskom paketu “ Matlab”, nalazimo vrednost ulaznog signala, koji je sada ≈1.7 puta veći u odnosu na sistem sa otvorenom povratnom spregom. Na osnovu izvedenog razmatranja i simulacija, zakjučujemo da i za ovakav pojačavač važi formula Ar=A/1-βA, što bi i praktično trebalo proveriti.
Slika 14. Odziv sistema za koeficijent povratne sprege k=1
Slika 15. Odziv sistema za koeficijent povratne sprege k=0.5 i povecanu vrednost amplitude ulaznog audio signala
Koeficijent korisnog dejstva pojačavača klase D
Izlazni stepen pojačavača klase D čini polumostni invertor koji radi u prekidačkom režimu. Zbog takvog načina rada možemo očekivati veći koeficijent korisnog dejstva η u odnosu na audio pojačavač sa push-pull izlaznim stepenom u klasi AB.
Za idealne prekidačke komponente, idealno filtarsko kolo i indeks modulacije M=1, u odeljku 3.1, prikazano je, da na izlazu pojačavača dobijamo maksimalnu amplitudu jednaku naponu napajanja Vo=Vcc. Pošto idealne prekidačke komponente nemaju gubitke, svu snagu koju uzimamo iz izvora predajemo potrošaču-zvučniku. U posmatranom, teoretskom slučaju, koeficijent korisnog dejstva,mogao bi iznositi η=100%. Naša korisna snaga data je sa:
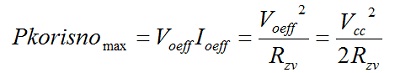
Realno posmatrano, ne postoje idealne prekidačke komponente, kao ni idealni filtri, pa će η sigurno biti manje od teoretsko dobijene vrednosti. Razlog pojave gubitaka potiče od samih prekidačkih komponenti, u našem slučaju od mos tranzistora i nesavršenosti pasivnih komponeti filtra.
Gubici na prekidačkim komponentama nastaju iz dva razloga:
• prvi je u nekoj maloj, ali konačnoj otpornosti kanala izmedju drejna i sorsa (Rdson) mos tranzistora. Kada radi kao prekidač, u provodnom stanju, moraju biti zadovoljeni uslovi Vgs>Vt i Vgd>Vt, da bi se nalazio u omskoj oblasti prenosne karakteristike. Pad napona na komponenti koja radi u omskoj oblasti odredjena je sa vrednosti Rdson. Tipične vrednosti Rdson današnjih komponenti je reda nx10mΩ. Gubitke nastale tokom vodjena mos-fetova obeležavamo sa Pon.
• drugi razlog je u vremenu koje je potrebno mos tranzistoru da provede po dovodjenju napona Vgs>Vt, a potom da se isključi po ukidanju napona gejta. U ovom prelaznom periodu postoji značajna struja kroz mos tranzistor kao i napon na njemu, uzrokujući disipaciju. Na samu disipaciju utiče, u velikoj meri i karakter opterećenja. Karakteristična vremena koja opisuju prelazne pojave kod mosfeta su: td-vreme kašnjena po dovodjenju pobude, tr-vreme porasta struje, ts-vreme kašnjenja po ukidanju pobude i tf-vreme opadanja struje tranzistora. U zavisnosti od snage i namene, ona se kreću u intervalu od 10ns do nekoliko desetina nx10ns (za energetske komponente). Razlog tome leži u kapacitativnosti izmedju gejta i sors i gejta i drejna (Cgs, Cgd), pa je potrebno neko vreme da se oni napune odnosno isprazne. Gubitke nastale tokom ovih vremena (tr i tf) nazivamo komutacionim gubicima Pcom.
Odrediti tačne vrednosti ovih gubitaka je teško. Otežavajući faktor je i sama priroda pobudnog audio signala. Zbog toga, prilikom ocene gubitaka, koristićemo se aproksimacijama za najgore slučajeve.
Pon gubitke nastale tokom provodjenja jednog mos tranzistora u k-tom intervalu periode Tm modulišućeg signala (Tm≈nxTc) , možemo približno odrediti kao:
Struje kroz mos tranzistore u posmatranim intervalima teško se nalaze, a vrednost Rdson provodnog mos tranzistora je mala naspram Rzv (Rdson je reda ≈ 50mΩ). Zbog toga ove gubitke možemo zanemariti.
Komutacioni gubici su dati sa:
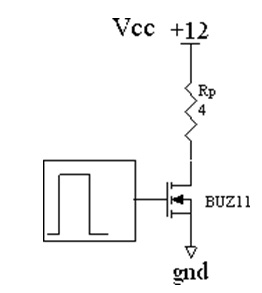
Ovo je neki uopšteni slučaj gde su uds(t) i id(t) funkcije odgovarajućih napona i struja mos tranzistora tokom prelaznog vremena uključenja (tpr.uklj), odnosno isključenja (tpr.isklj). Date funkcije u velikoj meri zavise od karaktera potrošašača, pa ovo predstavlja veliki problem pri analizi komutacionih gubitaka. Na slici 16, prikazano je uprošćeno prekidačko kolo koje ćemo analizirati pri prekidanju maksimalne struje potrošača, odredjene sa Ip=Vdd/Rp.
Slika 16.
Da bi mogli odrediti Pcom, pretpostavljamo da se tokom komutacije napon i struja menjaju linearno. Tada bi pri uključivanju mos tranzistora važilo:
Vremena tr i tf nalazimo iz kataloga za korišćeni mosfet.
Srednja vrednost snage disipirane tokom uključenja je:
Analogno, srednja disipirana snaga tokom isključenja je:
pa je srednja snaga komutacije za oba tranzistora data sa:
Pri izvodjenju smo zanemarili vremena td i ts jer smo usvojili da je disipacija na Rdson zanemarljiva u odnosu na Pcom.
Koeficijent korisnog dejstva dat je sa:
Za Vdd=12V, Rp=4Ω, M=1, fc=75kHz, tr=200ns i tf=110ns (BUZ11) možemo utvrditi orijentacionu vrednost koeficijenta korisnog dejstva η: Pkorisnomax=18W; Pcom=0,279W => η=98%
Za prekidačku učestanost fc=200kHz, koja zavisi od učestanosti nosećeg testerastog signala, dobili bi smo: η=96%. Vidimo da se povećanjem prekidačke učestanosti povećavaju komutacioni gubici i smanjuje η, kao i da smanjenjem izlazne snage, η opada, jer su komutacioni gubici Pcom konstantni, bez obzira na izlaznu snagu u našem aproksimiranom slučaju. U realnom slučaju, indeks modulacije morao bi biti nešto manji od M<1, tako da je realno očekivati koeficijent korisnog dejstva od η=85%-90%, zbog svih aproksimacija koje smo uveli.
Ovo je razlog, zbog kojeg bi u budućnosti, usavršavanjem prekidačkih komponenti, pojačavači klase D mogli zameniti do sada korišćene push-pull izlazne pojačavače snage klase AB.
 Audiopojačavači klase D se razlikuju od ostalih klasa jer rade na potpuno drugačijem principu. Ovu vrstu pojačavača nazivaju i “digitalni” pojačavači, zbog samog oblika signala, iako se pod digitalnim pojačavačima smatraju sklopovi koji pojačavaju digitalni signal. Pojačavači klase D se baziraju na široko-impulsnoj modulaciji. Trajanje poluperioda pravougaonog signala zavisi o vrednosti analognog nisko-frekventnog signala. Na izlazu iz modulatora se nalazi pravougaoni signal sa samo dve vrednosti.
Audiopojačavači klase D se razlikuju od ostalih klasa jer rade na potpuno drugačijem principu. Ovu vrstu pojačavača nazivaju i “digitalni” pojačavači, zbog samog oblika signala, iako se pod digitalnim pojačavačima smatraju sklopovi koji pojačavaju digitalni signal. Pojačavači klase D se baziraju na široko-impulsnoj modulaciji. Trajanje poluperioda pravougaonog signala zavisi o vrednosti analognog nisko-frekventnog signala. Na izlazu iz modulatora se nalazi pravougaoni signal sa samo dve vrednosti.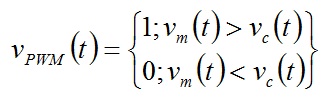
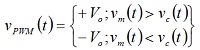
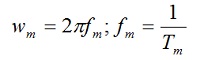
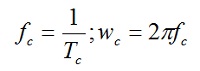
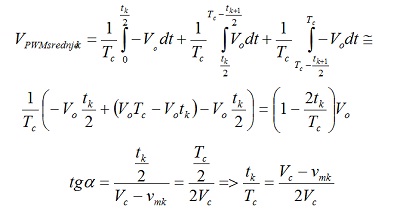
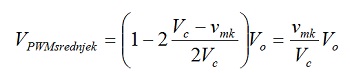
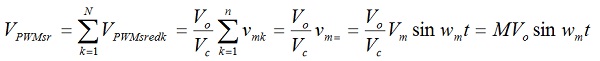
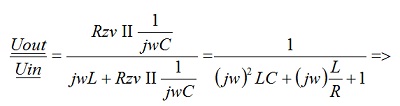
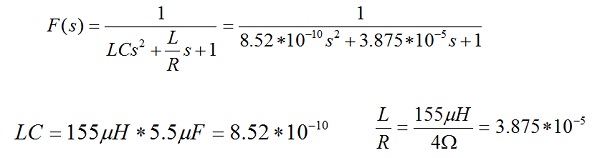
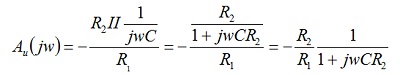
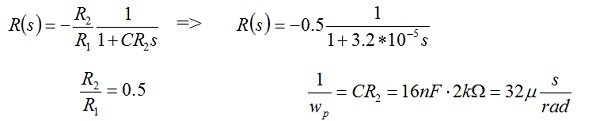
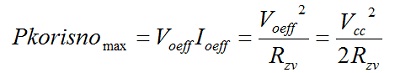
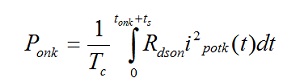
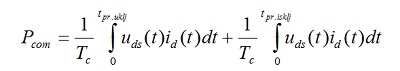
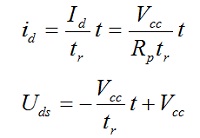
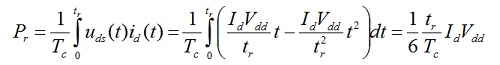
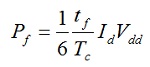
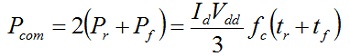
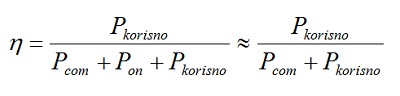





















![Da li je robot golman toliko dobar ili su loši izvođači? [VIDEO]](https://www.automatika.rs/wp-content/uploads/2012/05/hqdefault-1-218x150.jpg)