Uvod u neuralne mreže

Neuralne mreže (Neural Networks – NN) predstavljaju novu generaciju sistema za informaciono procesiranje koje pokazuju osobinu učenja, memorisanja i generalizacije na osnovu podataka kojima se obučavaju. Pokazuje se da su vrlo  efikasne u zadacima kao što su mečovanje i klasifikacija oblika, aproksimacija funkcija, optimizacija, vektorska kvantizacija, klasterizacija podataka, dok su konvencionalni računari, zbog svoje arhitekture vrlo neefikasni, pogotovo u domenu mečovanja oblika. Istini za volju, konvencionalni računari su brži uračunskim algoritmima i preciznim aritmetičkim operacijama.

 OSNOVNI KONCEPT NEURALNIH MREŽA

Neuralne mreže (Neural Networks – NN) predstavljaju novu generaciju sistema za informaciono procesiranje koje pokazuju osobinu učenja, memorisanja i generalizacije na osnovu podataka kojima se obučavaju. Pokazuje se da su vrlo  efikasne u zadacima kao što su mečovanje i klasifikacija oblika, aproksimacija funkcija, optimizacija, vektorska kvantizacija, klasterizacija podataka, dok su konvencionalni računari, zbog svoje arhitekture vrlo neefikasni, pogotovo u domenu mečovanja oblika. Istini za volju, konvencionalni računari su brži u računskim algoritmima i preciznim aritmetičkim operacijama.

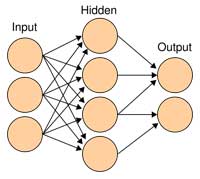
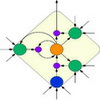
Neuralne mreže se sastoje  od velikog broja gusto povezanih procesorskih elemenata (takozvanih  čvorova, ‘nodes’) koji uobičajeno rade u paraleli (jednovremeno) i  koji su organizovani po nekim regularnim arhitekturama. Razvoj neuralnih mreža je nastao motivacijom da se modeliuje ponašanje (bioloških) neurona u mozgu. Zbog toga se vrlo  često neuralnim mrežama dodaje atribut ‘veštačke’ neuralne mreže (Artificial Neural  Networks – ANN), pa se stoga i čvorovi odnosno procesorski elementi  često nazivaju veštačkim neuronima, ili samo neuronima. Ljudski mozak se sastoji od otprilike 10^11 neurona različitih tipova.  Na slici je prikazan jednostavni matematički model biološkog neurona koji su predložili McCulloch i Pitts davne 1943. godine i koga su nazvali M-P neuron.

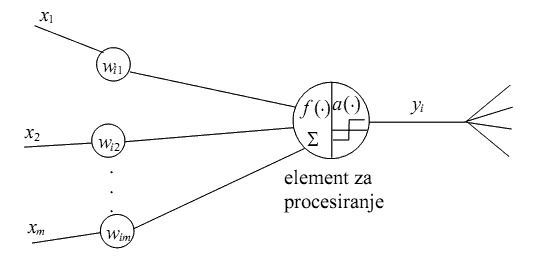
U ovom modelu i-ti element za procesiranje računa težinsku sumu ulaza i kao izlaz generiše signal  y_i= 1 ili  y_i= 0 u zavisnosti od toga da li je težinska suma veća ili manje od nekog unapred definisanog praga Θ_i:

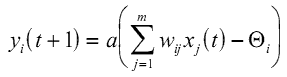
gde je aktivaciona fukcija a(f) jedinična step funkcija:

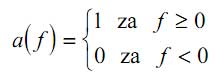
Težine w_ij predstavljaju snagu sinapse odnosno veze između neurona  j (izvora) i neurona  i (destinacije). Pozitivna težina predstavlja eksitornu sinapsu, a negativna težina predstavlja inhibirajuću sinapsu. Ako je w_ij= 0 između ova dva neurona veza ne postoji. U jednačini koja opisuje funkcionisanje elementa za procesiranje se pretpostavlja da postoji transportno kašnjenje od trenutka dolaska signala na ulaz do generisanja izlaznog signala i ovi su trenuci označeni sa  t  i  t+1. Iako
jednostavan, MP model neurona ima neverovatne računarske potencijale. On može da realizuje bazične logičke operacije NOT, OR i AND ukoliko se pragovi u elementima za procesiranje izaberu na odgovarajući način. To znači da se odgovarajućim spregama dovoljno velikog broja ovakvih neurona može u potpunosti realizvoati funkcija univerzalnih računara.

U skladu sa napred rečenim neuralna mreža se može definisati kao paralelna distribuirana struktura za procesiranje podataka (informacija) koja poseduje sledeće osobine:

1) To je matematički model inspirisan biološkim nervnim sistemom;

2) Sastoji se od velikog broja vrlo povezanih elemenata za procesiranje;

3) Znanje je sadržano u težinama odnosno vezama između čvorova;

4) Element za procesiranje dinamički odgovara na ulazni stimulus, i pri tome je ovaj odgovor kompletno zavisan od lokalne informacije sadržane u njegovom okruženju;

5) NN ima osobinu da uči, pamti i generalizuje na osnovu obučavajućeg
skupa;

6) Zajedničko ponašanje svih delova mreže predstavlja kompjutersku snagu, ali to svojstvo ne sadrže usamljeni čvorovi ponaosob.

OSNOVNI MODELI I PRAVILA OBUČAVANJA NEURALNE MREŽE

 Model neuralne mreže je određen sa tri svojstva. Prvo od njih je model elemenata za procesiranje odnosno  čvorova, drugo je veza između čvorova i njihova struktura i treće važno svojstvo koje definiše prirodu mreže je pravilo za obučavanje kojim se podešavaju težine na pojedinim vezama.

Elementi za procesiranje
Funkcionisanje MP neurona se može proširiti na generalni model elementa za procesiranje. Informacija koju procesira  čvor se može podeliti na ulazni i izlazi signal. Zapravo, vrlo važnu vezu između ulaznog i izlaznog signala u  i-tom  čvoru predstavlja integraciona funkcija  f_i koja je pridružena posmatranom  čvoru i govori o tome na koji način ulazni signali formiraju zajedničkog reprezenta. Na primeru MP neurona, u pitanju je linearna funkcija ulaznih signala  x_j:

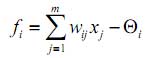
 gde je Θ_i  prag i-tog čvora. Nešto složeniji oblici integracionih funkcija su sledeći:

1. Kvadratna funkcija ulaznih signala x_j: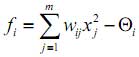

2. Sferična funkcija ulaznih signala x_j: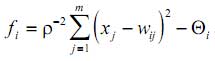

3. Polinomska funkcija ulaznih signala x_j: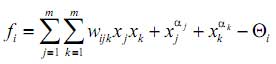

Sledeća aktivnost elementa za procesiranje jeste da se zbirni reprezent ulaznih signala  f_i prenese do izlaza čvora u obliku izlaznog signala. Za to je zadužena takozvana aktivaciona funkcija ili funkcija prenosa a(f) . Neki uobičajeni oblici aktivacionih funkcija su sledeći:

1. Step funkcija:

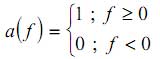
 2. Hard limiter:

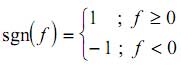
3. Funkcija rampe: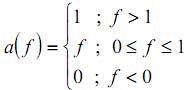

  4. Unipolarna sigmoidalna funkcija:

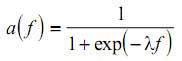
5. Bipolarna sigmoidalna funkcija: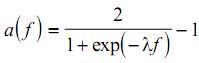

gde je λ>0  i ovaj parametar određuje strminu sigmoidnih funkcija. Za vrlo male vrednosti ovog parametra sigmoidna funkcija teži ka linearnoj, dok je za veliku vrednost parametra ova funkcija vrlo slična funkciji hard limita.
Nelinearne integracione funkcije ulaznih signala omogućavaju kompleksne particije prostora obeležja koje se nazivaju  granicama odluke (po analogiji sa prepoznavanjem oblika, a zapravo označava termin da se može formirati krajnje nelinearne granica separacije između dveju klasa). Međutim, što je složenija integraciona funkcija, to mora biti složenija i interakcija između čvorova u neuralnoj mreži.

Veze između čvorova

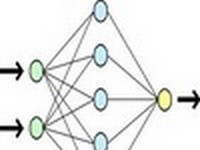
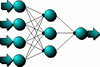
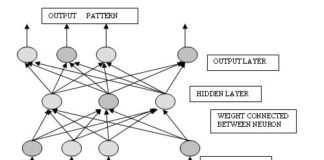
Neuralna mreža se sastoji od velikog broja  čvorova koji su gusto povezani kako sa drugim čvorovima, tako i sa samim sobom, pri čemu je dozvoljeno i kašnjenje u propagaciji signala kroz  čvorove.  Na sledećoj slici je prikazno pet bazičkih struktura neuralnih mreža, odnosno pet bazičnih, takozvanih geometrija veza među čvorovima.

 Jednoslojna feedforward mreža

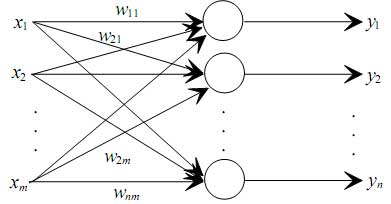
 Jednoslojna rekurentna mreža

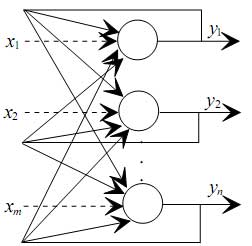
 Čvor sa sopstvenom povratnom spregom

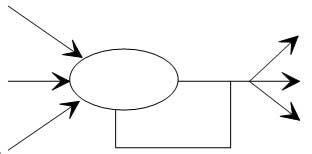
 Višeslojna rekurentna mreža

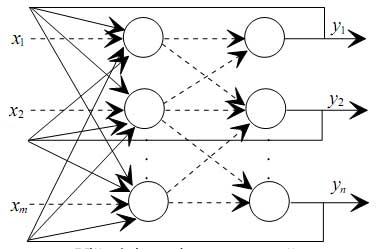
 Višeslojana feedforward mreža 

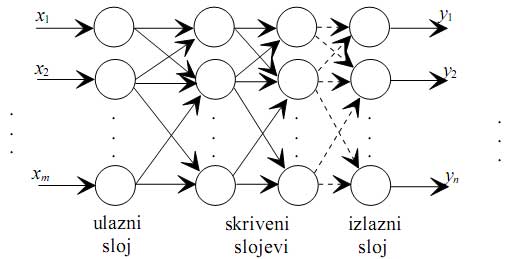
Za početak se sa ovih struktura mreža vidi da se uvek više  čvorova ogranizuje po slojevima, pri čemu u svaki od čvorova ulazi više ulaznih signala sa različitim težima, a da tada iz sloja imamo više izlaznih signala, po jedan za svaki čvor. Broj slojeva u mreži može biti jedan ili veći, te se na taj način razlikuju jednoslojne od višeslojnih mreža. Dalje se vidi da kod višeslojnih mreža prvi sloj zapravo predstavlja ulazni sloj i on nema nikakvu drugu funkciju već da ulazne signale multiplicira onoliko puta kolike su potrebe prvog sledećeg sloja. Izlazi iz mreže se generišu iz izlaznog sloja. Svaki sloj čvorova između ulaznog i izlaznog se naziva skriveni sloj. U neuralnoj mreži broj skrivenih čvorova može  biti od nula do nekoliko. Za neuralnu mrežu se kaže da je  potpuno povezana  ako je svaki  čvor iz prethodnog vezan za svaki  čvor iz
sledećeg sloja. Dalje se može primetiti da se u navedenim strukturama razlikuju dva tipa mreža. Prvi tip mreža su takozvane  feedforward mreže kod kojih se izlazi iz čvorova ne vraćaju kao ulazi u čvorove iz istog ili prethodnih slojeva. Za razliku od feedforward mreže, feedback mreže (mreže sa povratnom spregom) imaju tu osobinu da se izlazi iz čvorova vraćaju kao ulazi u  čvorove istog ili prethodnih slojeva. Povratna sprega u kojoj se izlazi iz čvorova vraćaju na ulaze čvorova iz istog sloja se naziva  lateralna povratna sprega. Feedback neuralne mreže koje imaju zatvorene petlje se nazivaju rekurentnim neuralnim mrežama.

Tekst je preuzet iz skripte Prof. Željka Đurovića za predmet Prepoznavanje govora