Važna oblast primene neuralnih mreža je oblast robotike. Uobičajeno, ove mreže su projektovane da usmere robotski manipulator, koji predstavlja najznačajniji oblik industrijskog robota, da uhvati objekat na osnovu podataka koje mu daju senzori. Druge primene uključuju upravljanje i planiranje putanje autonomnog robotskog vozila.
U robotici, glavni zadatak podrazumeva pravljenje pomeraja u zavisnosti od senzorskih podataka. Ovde se javljaju četiri povezana problema koje treba razlikovati:
1. Ravna kinematika
Kinematika je nauka o kretanju koja tretira kretanje bez razmatranja sila koje se pri tome stvaraju. U okviru ove nauke se proučavaju pozicija, brzina, ubrzanje i svi izvodi višeg reda koji se odnose na promenjive pozicije. Prilično osnovni problem u proučavanju mehaničkog manipulisanja je ravna kinematika. To je statički geometrijski problem proračuna pozicije i orjentacije zadnjeg efektora („ruke“) manipulatora. Specifično, dat je skup zajedničkih uglova i problem ravne kinematike je da izračuna poziciju i orjentaciju okvira alata relativno na okvir osnove.
Slika 1. Primer robotskog manipulatora
2. Inverzna kinematika
Ovaj problem može da se predstavi na sledeći način: data je pozicija i orjentacija zadnjeg efektora manipulatora i potrebno je proračunati sve moguće skupove zajedničkih uglova koji bi mogli da budu iskorišćeni za postizanje date pozicije i orjentacije. Ovo je, zapravo, osnovni problem u praktičnoj primeni manipulatora. Problem inverzne kinematike robota nije tako jednostavan kao problem ravne kinematike robota. Zbog toga što su kinematske jednačine nelinearne, njihovo rešenje nije uvek jednostavno ili čak moguće u zatvorenom obliku. Takođe, nameće se pitanje da li rešenje postoji ili postoji više rešenja. Rešavanje ovog problema je poslednji zahtev za većinu robotskih upravljačkih sistema.
3. Dinamika
Dinamika je oblast mehanike koja je posvećena proučavanju sila koje prouzrokuju kretanje. Sa ciljem da se ubrza manipulator, učini klizanje na konstantnog brzini zadnjeg efektora i konačno uspori i zaustavi, kompleksan skup funkcija momenta mora da se primeni u slučaju zajedničkih aktuatora. U dinamici se ne koriste samo geometrijske osobine (kinematika), već i fizičke osobine robota se uzimaju u razmatranje. Uzmimo, na primer, težinu (inerciju) robotske ruke, koja određuje silu potrebnu da promeni kretanje ručice. Dinamika uvodi dva dodatna problema problemima kinematike.
- Robotska ruka ima ‘memoriju’. Njeni odgovori na upravljački signal zavise takoñe od njene istorije (na primer, prethodne pozicije, brzine, ubrzanja).
- Ukoliko robot uzima objekat, dinamika se menja, ali kinematika ne. To je zato što masa objekta mora da bude dodata na masu ručice (upravo zbog toga su robotske ručice tako teške, čineći relativnu težinu vrlo malom).
4. Generisanje trajektorije
Da bi se pomerio manipulator sa jednog mesta na drugo na gladak, kontrolisan način, svaka veza mora da se pomeri po glatkoj funkciji vremena. Upravo je način računanja ove funkcije kretanja problem generisanja trajektorije. U daljem tekstu će biti data diskusija problema vezanih za pozicioniranje zadnjih efektora.
Pozicioniranje zadnjeg efektora
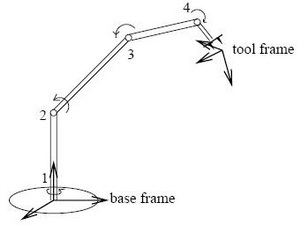
Konačni cilj pri upravljanju robotskim manipulatorom je pozicioniranje zadnjeg efektora ili robotske ruke sa ciljem da se, na primer, pokupi objekat. Sa preciznom robotskom rukom, ovaj zadatak je relativno jednostavan i uključuje sledeće korake:
- Određivanje koordinata cilja relativno u odnosu na osnovu robota. Tipično, kada ova pozicija nije uvek ista, ovo se ostvaruje pomoću odreñenog broja fiksiranih kamera ili drugih senzora koji posmatraju scenu tako da se iz okvira slike odreñuje pozicija objekta u toj slici i izvršava pre-odreñivanje koordinantnih transformacija;
- Sa preciznim modelom robota, izračunava se ugao veza koje dostižu cilj (na primer, inverzna kinematika). Ovo je relativno jednostavan problem;
- Pomeranje robotske ruke i približavanje držača.
Dakle, ako je sve ovo lako rešiti sa visokom tačnošću, zbog čega u sve uključiti i neuralne mreže? Razlog leži u primenjivosti robota. Kada se koriste ‘tradicionalne’ metode za upravljanje robotskom rukom, tačni modeli senzora i manipulatora su zahtevani i sam sistem mora da bude baždaren. Takoñe, sistemi koji se lako troše i habaju, zahtevaju čestu kalibraciju i odreñivanje parametara. Konačno, sa razvojem složenijeg adaptivnog upravljanja došlo je do razvoja fleksibilnijih robotskih sistema, kako sa senzorske, tako i sa motorne strane.
Pristup 1: Mreže sa pozitivnom povratnom spregom
Kada se koristi sistem sa pozitivnom povratnom spregom za upravljanje manipulatorom, potrebno je koristiti sistem sa sopstvenim nadzorom učenja. Jedan takav sistem je bio opisan od strane Psaltis, Sideris i Yamamura (Psaltis, Sideris, & Yamamura, 1988). Ovde, mreža, koja je konzistentna 20dimenzinalnom pozicioniranju robotske ruke, uči na osnovu eksperimenata. Predložene su tri metode:
i. Indirektno učenje
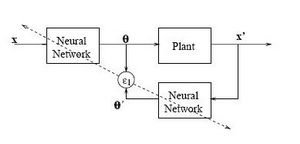
U indirektnom učenju, Dekartova ciljana tačka x se generiše u koordinantnom sistemu, na primer, pomoću dve kamere koje posmatraju objekat. Ova ciljana tačka je napajana u mreži, koja generiše ugaoni vektor θ. Manipulator se pomera na poziciju θ, i kamera odreñuje novu poziciju x’ zadnjeg efektora u koordinantnom sistemu. Veličina x’ je ponovo ulaz za mrežu, koji rezultira u ugao θ’. Mreža je tada trenirana na grešku ε1= θ-θ’.
Slika 2. Indirektno učenje za robotiku. U svakom ciklusu, mreža se koristi na dva različita mesta: prvo u
koraku napred, i zatim kao povratna sprega greške.
Međutim, minimizacija greške ε1 ne garantuje minimizaciju celokupne greške ε = x-x’. Na primer, mreža se obično podešava na ‘rešenje’ koje mapira sve x’ vrednosti na jedinstvenu vrednost θ.
ii. Opšte učenje
Metod je u osnovi vrlo sličan nadziranom učenju, ali ovde ulaz objekta θ mora biti obezbeđen od strane korisnika. Tako mreža može direktno da minimizira |θ – θ’|. Uspeh ove metode zavisi od sposobnosti interpolacije mreže. Pravilan izbor ugla θ može da pojednostavi problem.
iii. Specijalizovano učenje
Treba imati u vidu da je cilj treninga mreže minimiziranje greške izlaza objekta: ε = x – x’. Takođe je moguće trenirati mrežu pomoću ‘back-propagacije’ greška kroz objekat . Ova metoda zahteva poznavanje Jakobijanovih matrica objekta upravljanja. Jacobijanova matrica multidimenzionalne funkcije F je matrica parcijalnih izvoda funkcije F, odnosno multidimenzionalna forma izvoda.
Sada, u ovom slučaju imamo Pi( θ ), i0ti element izlaza objekta za ulaz θ. Pravilo učenja koje se primenjuje ovde se odnosi na objekat kao dodatni i jednorežimski sloj u neuralnoj mreži. Ukupna greška ε = x – x’ se prostire nazad kroz objekat.
Dvoslojna mreža sa pozitivnom povratnom spregom se trenira pomoću back0propagacije. Međutim, umesto računanja željenog vektora izlaza koji bi trebao da uvede trenutni vektor izlaza i da ga rekonstruiše, primenjena je back0propagacija na ovaj novi vektor ulaza i postojeći vektor izlaza. Korišćena konfiguracija se sastoji od monokularnog manipulatora koji hvata objekte. Zbog činjenice da je kamera pozicionirana na ruci robota, zadatak je da se pomeri ruka tako da je objekat u centru slike i da ima predefinisanu veličinu (Smagt, Krose, & Groen, 1992) pri kojoj se koristi vizuelno polje za proračun monokularnosti sistema. Jedan korak napred prema cilju se sastoji od sledećih operacija:
- Merenje rastojanja od trenutne pozicije do same pozicije cilja u domenu kamere, x.
- Korišćenje rastojanja, zajedno sa trenutnim stanjem θ robota, kao ulaza za neuralnu mrežu. Mreža
tada generiše rastojanje veze Cθ. - Slanje Cθ manipulatoru.
- Ponovno mernje rastojanja od trenutne pozicije do pozicije cilja u domenu kamere, x’.
- Izračunavanje pomeraja manipulatora u vizuelnom domenu, gde je rotaciona matrica druge slike kamere sa tolerancijom u odnosu na r-tu sliku kamere;
- Učenje neuralne mreže.
Korišćenjem mreže sa pozitivnom povratnom spregom, dostupni uzorci za učenje se približno predstavljaju kao pojedinačna, glatka funkcija koja se sastoji od sume sinusnih funkcija. Ovakva mreža sa jednim slojem sinusnih jedinica je sposobna da predstavi praktično bilo koju funkciju. Ali, kakvi su optimalni težinski koeficijenti odreñeni u konačnom vremenu koji postižu optimalnu reprezentaciju? Eksperimenti su pokazali da razumna reprezentacija može da se postigne u kratkom periodu vremena, dok tačna reprezentacija funkcije koja upravlja uzorkom učenja je obično nemoguće ili ekstremno komplikovana. Razlog za ovo predstavlja opšti karakter aproksimacije koji se postiže mrežom sa pozitivnom povratnom spregom koja ima sinusne jedinice: svaki težinski koeficijent u mreži ima globalne efekte na konačnu aproksimaciju. Građenje lokalnih reprezentacija je očigledan izlaz iz ove situacije: svaki deo mreže je odgovoran za mali potprostor ukupnog prostora ulaza. Na taj način, tačnost je postignuta lokalno. Ovo se tipično postiže pomoću Kohonen-ove neuralne mreže.
Pristup 2: Topologija koja konzervira mape
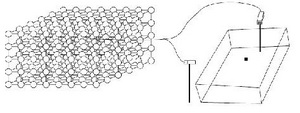
Opisani sistem se sastoji od robotskog manipulatora sa 3 stepena slobode koji je u stanju da uhvati objekat u 3D-prostoru. Sistem se posmatra pomoću dve fiksirane kamere koje predstavljaju izlaz njihovih (x; y) koordinata u smislu objekta i zadnjeg efektora.
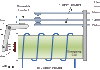
Slika 3. Kohonen-ova mreža koja se odnosi na izlaz dveju kamera.
Svako kretanje se satoji od dva pokreta. U ukupnom pokretu, posmatrana lokacija objekta x je ulaz mreže. Pomoću Kohonen-ove neuralne mreže, neuron k sa najvišom vredošću aktivacije je selektovan kao pobednik, zato što je njegov težinski vektor Wk najbliži vrednosti x. Neuroni, koji su rasporeñeni u 3D rešetki, koresponduju na 1-1 način sa podregionom 3D radnog prostora robota, odnosno neuronalna rešetka je diskretna reprezentacija radnog prostora. Sa svakim neuronom, vektor θ i Jacobijanova matrica A su pridruženi. Za vreme ukupnog pomeraja, ugao θk se dovodi do robota koji zatim načini pokret koji rezultira u promenu koordinata zadnjeg efektora.
