Sistem brojeva je sistematičan način predstavljanja brojeva pomoću simboličkih znakova i koristi osnovnu vrednost kako bi se brojevi praktično grupisali u sažetom obliku. Najčešći sistem brojeva jeste decimalni, koji ima osnovnu vrednost 10, a simbolički skup znakova od 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Međutim, postoje i drugi sistemi brojeva i oni mogu biti efikasniji za određene svrhe.

 Heksadecimalni (šesnaestični) sistem je uveden da bi se prevazišao problem dužine binarnog zapisa. Heksadecimalni zapis zahteva manje cifara, što je mnogo prihvatljivije za čoveka. U matematici i informatici se često koristi heksadecimalni brojevni sistem, iako računar operiše nad binarnim brojevima, oni se mogu jednostavno prevesti u heksadecimalni oblik zahvaljajući pogodnom odnosu osnova ova dva sistema (24 = 16).

 Heksadecimalni brojni sistem ima 16 cifara (heksa na grčkom znači šestnaest). To je brojni sistem koji u osnovi ima 16, odnosno sistem sa 16 različitih znakova, od čega su 10 arapskih cifara i dodaju se slova od A do F. Znak A odgovara decimalnom broju 10, …, a F decimalnom broju 15.

Konverzija dekadnog broja u heksadecimalni

Evo primera kako da konvertujete broj A2F u odgovarajući broj dekadnog brojnog sistema.

{\displaystyle A2F(16)=A\times 16^{2}+2\times 16^{1}+F\times 16^{0}=10\times 256+2\times 16+15\times 1=2607}

{\displaystyle A2F_{(16)}=2607_{(10)}\,}

Prebacivanje dekadnog u heksadecimalni

{\displaystyle 2607/16=162\,}

 (ostatak 15, odnosno F)

{\displaystyle 162/16=10\,} (ostatak 2)

{\displaystyle 10/16=0\,} (ostatak 10, odnosno А)

I tako dobijamo da je :

2607(10)=A2F(16)

Konverzija binarnog broja u heksadecimalni

 Heksadecimalni broj 4A2 trebamo da prevedemo u binarni oblik. Znači da svaku heksadecimalnu cifu prevedemo u binarni oblik.

Dakle, 4A2 heksadecimalno je 100101010 binarno, jer:

  • 4 je 100
  • A je 1010
  • 2 je 10

pa kad ova tri binarna niza spojimo dobijamo 100101010.

Prebacivanje binarnog u heksadecimalni

 Ako želimo da neki binarni broj prevedemo u hesadecimalni oblik, sve što treba da uradimo je da binarni broj razdelimo u grupe od po četiri cifre (počev s desna) i svaku grupu prevedemo u heksadecimalnu cifru.

 Uzmimo za primer binarni broj 1000101010101110100100111. Najpre broj razdelimo u grupe od po četiri cifre:

1 0001 0101 0101 1101 0010 0111

Sada svaku grupu prevedimo u heksadecimalnu cifru:

1 prevodimo u 1
0001 prevodimo u 1
0101 prevodimo u 5
0101 prevodimo u 5
1101 prevodimo u D (13)
0010 prevodimo u 2
0111 prevodimo u 7

Pa je tako 1000101010101110100100111 binarno jednako 1155D27 heksadecimalno.

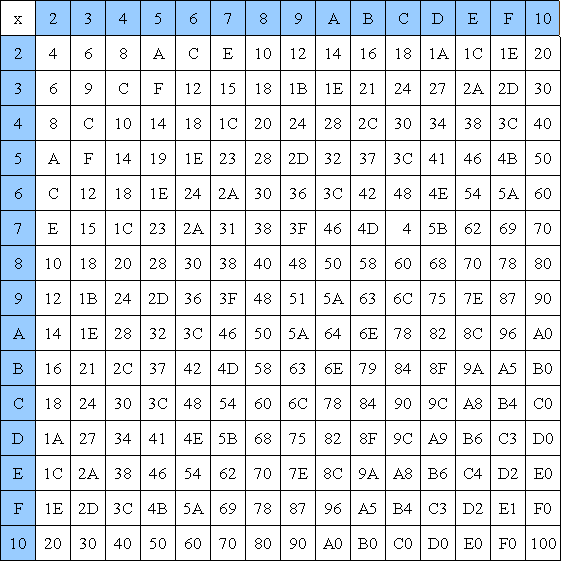
Tabela br.1 Tablica mnozenja u heksadecimalnom sistemu brojeva

 Heksadecimalni sistem je pogodno koristiti u računarima pošto je pretvaranje između binarnog i heksadecimalnog sistema veoma jednostavno. Tako se svaka četiri bita mogu napisati kao jedna cifra heksadecimalnog sistema, što znači da se jedan bajt može napisati kao dve cifre u heksadecimalnom sistemu.

 Heksadecimalni sistem u upotrebu je uvela kompanija IBM 1963. godine.

 

 

POVEZANI ČLANCIVIŠE OD AUTORA

1 KOMENTAR

  1. Konverzija binarnog broja u heksadecimalni
    Heksadecimalni broj 4A2 trebamo da prevedemo u binarni oblik. Znači da svaku heksadecimalnu cifu prevedemo u binarni oblik.

    Dakle, 4A2 heksadecimalno je 100101010 binarno, jer:

    4 je 100
    A je 1010
    2 je 10
    pa kad ova tri binarna niza spojimo dobijamo 100101010.
    Ovo gore nije tacno!
    4 je 0100 (posto je prvi broj prva nula se moze ignorisati pa cemo ga napisati kao 100)
    A je 1010
    2 je 0010
    4A2 je 10010100010

POSTAVI ODGOVOR

Please enter your comment!
Please enter your name here

This site uses Akismet to reduce spam. Learn how your comment data is processed.