Da bi se proširila klasa signala čiju je frekvencijsku reprezentaciju moguće definisati preko matematičkih funkcija uvedena je Laplace-ova transformacija, isto tako, u analizi i sintezi sistema uopšte, pojavljuje se problem rešavaja diferencijalnih jednačina. Analiza ponašanja linearnih dinimičkih sistema sa koncetrisanim i vremenskim nepromenljivim parametima se svodi na problem rešavanja odgvarajućeg sistema linearnih diferencijalnih jed. sa konstantnim koeficijentima. Rešavanje ovih jednačina se pojednostavljuje primenom Laplace-ove transformacije.
proširila klasa signala čiju je frekvencijsku reprezentaciju moguće definisati preko matematičkih funkcija uvedena je Laplace-ova transformacija, isto tako, u analizi i sintezi sistema uopšte, pojavljuje se problem rešavaja diferencijalnih jednačina. Analiza ponašanja linearnih dinimičkih sistema sa koncetrisanim i vremenskim nepromenljivim parametima se svodi na problem rešavanja odgvarajućeg sistema linearnih diferencijalnih jed. sa konstantnim koeficijentima. Rešavanje ovih jednačina se pojednostavljuje primenom Laplace-ove transformacije.
 proširila klasa signala čiju je frekvencijsku reprezentaciju moguće definisati preko matematičkih funkcija uvedena je Laplace-ova transformacija, isto tako, u analizi i sintezi sistema uopšte, pojavljuje se problem rešavaja diferencijalnih jednačina. Analiza ponašanja linearnih dinimičkih sistema sa koncetrisanim i vremenskim nepromenljivim parametima se svodi na problem rešavanja odgvarajućeg sistema linearnih diferencijalnih jed. sa konstantnim koeficijentima. Rešavanje ovih jednačina se pojednostavljuje primenom Laplace-ove transformacije.
proširila klasa signala čiju je frekvencijsku reprezentaciju moguće definisati preko matematičkih funkcija uvedena je Laplace-ova transformacija, isto tako, u analizi i sintezi sistema uopšte, pojavljuje se problem rešavaja diferencijalnih jednačina. Analiza ponašanja linearnih dinimičkih sistema sa koncetrisanim i vremenskim nepromenljivim parametima se svodi na problem rešavanja odgvarajućeg sistema linearnih diferencijalnih jed. sa konstantnim koeficijentima. Rešavanje ovih jednačina se pojednostavljuje primenom Laplace-ove transformacije.
Laplasova transformacija funkcije f(t) se definiše na sledeći način:
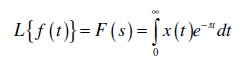
gde se kompleksna promenljiva s=δ+jω naziva kompleksna učestanost (frekvencija), a realni deo kompleksne promenljive s, Re{s}=δ, je izabran da obezbeđuje konvergenciju integrala. Laplace-ova transformacija definisana gornjim izrazom naziva se bilateralna ili dvostrana Laplace-ova transformacija. Dvostrana Laplace-ova transformacija koristi se za analizu elektroenergetskih sistema, kao i u izvesnim primenama u telekomunikacijama i obradi signala.
Za analizu kauzalnih signala ( x(t) = 0 za t<0 ), koji se prenose i obrađuju linearnim vremenski-invarijantnim kauzalnim ( fizički ostvarljivim ), realnim sistemima, fundamentalnu ulogu ima unilateralna ili jednostrana Laplace-ova transformacija, koja je definisana sa izrazom:
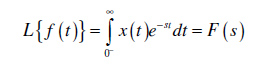
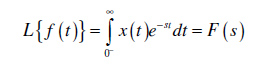
Ponekad se u literaturi unilateralna ( jednostrana ) Laplace-ova transformacija definiše kao:
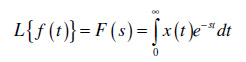
Razlika između ove dve definicije je samo u donjoj granici integracije, koja je kod prve definicije 0–, i ako signal x(t) ne sadrži impulsni delta signal δ(t) u koordinatnom početku ( t=0 ), ove dve su u osnovi identične. Međutim, ukoliko signal x(t) sadrži impulsnu delta funkciju u tačku t=0, neophodno je da definicioni integral obuhvati celokupni delta impuls, tako da donja granica integracije mora biti t=0–. Primetimo, takođe, da je Laplace-ova transformacija uvedena u teoriji linearnih vremenski-invarijantnih sistema prevashodno u cilju određivanja odziva ovakvog sistema na proizvoljnu eksitaciju, pa samim tim i na impulsnu delta pobudu. Sa druge strane, kao što je već istaknuto, odziv linearnog vremenski-invarijantnog ( stacionarnog ) sistema sastoji se iz dve komponenete ( tzv. princip superpozicije ): odziv na pobudu ( ulazni signal ili eksitaciju ) i odziva na početne uslove, koji predstavljaju nagomilanu energiju u sistemu pre dovođenja same pobude. Ako pretpostavimo da je t=0 vremenski trenutak u kome dovodimo pobudu na ulaz sistema, tada početni uslovi moraju biti definisani neposredno pre dovođenja eksitacije, odnosno za t=0–. Dakle, prva definicija Laplace-ove transformacije obezbediće određivanje odziva sistema kako na kauzalni ulazni signal tako i na početne uslove.
Osobine Laplace-ove transformacije
Teorema linearnosti:
- Homogenost: L{af(t)} = aF(s); gde je a realna konstanta
- Aditivnost: L{f1(t)+f2(t)} = F1(s)+F2(s)
- Linearnost: L{a1f1(t)+a2f2(t)} = a1F1(s)+a2F2(s)
Čisto vremensko kašnjenje:
- Za dve funkcije istog oblika f(t) i f(t-t0) gde druga kasni za prvom za vreme T, se može definisati: L{f(t-t0)} = e-st0F(s)
Primer funkcija sa čistim vremenskim kašnjenjem je trofazni sistem naizmeničnih struja.
Pomeranje kompleksnog lika:
- Pogodno za određivanje LT funkcija koje sadrže eksponencijalni faktor e-at : L{e-atf(t)} = F(s+a)
Skaliranje:
- Teorema o promeni vremenske skale: L{f(t/a)} = aF(as)
Konvolucija originala:
- Računska operacija konvolucije se definiše na sledeći način:
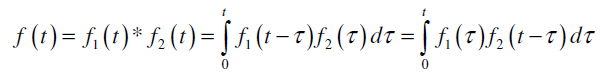
Laplasova transformacija konvolucije se definiše na sledeći način:
Teorema o izvodu originala: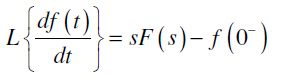
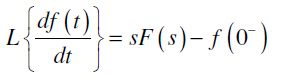
- Laplasova transformacija prvog izvoda funkcije f(t) se definiše kao:
gde je f(0–) početna vrednost funkcije f(t) u trenutku 0–. Laplasova transformacija n-tog izvoda funkcije f(t) se definiše kao:
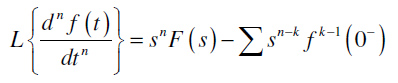
gde je fk-1(0–) početna vrednost k-prvog izvoda funkcije f(t) u trenutku 0–.
Primer:
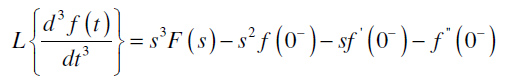
Teorema o integralu originala:
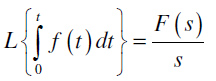
Za n-tostruki integral važi:
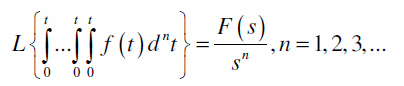
Teorema o izvodu kompleksnog lika:
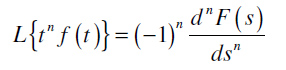
Prva granična teorema:
- Važi uz uslov da ne postoji impuls u koordinatnom početku
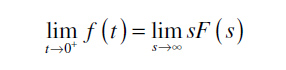
Druga granična teorema:
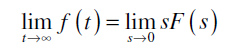
Na slici 1. možete videti Laplace-ove transformacije često korišćenihsignala, dok tabelu Laplace-ovih transformacija možete preuzeti naovom linku .

Slika 1. Laplace-ova tabela
Inverzna Laplace-ova transformacija
Na osnovu poznatog kompleksnog lika moguće je primenom inverzne Laplace-ove transformacije odrediti funkciju (original) u vremenskom domenu. Original funkcije F(s) u vremenskom domenu f(t) se određuje primenom sledećeg obrasca:
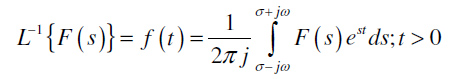
prethodna relacije se obično inverznom Laplace-ovom transformacijom, i zajedno sa relacijom:
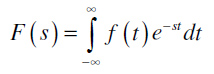
definiše takozvane Laplace-ove transformacione parove. Činjenica da funkcije f(t) i F(s) zadovoljavaju ove dve relacije, se često u literaturi označava jednom od sledećih notacija:
formula inverzne Laplace-ove transformacije nam kaže da se signal f(t) može rekonstruisati na osnovu njegovog Laplace-ovog transformacionog para, međutim, sračunati ovaj integral je vrlo često ozbiljan posao i podrazumeva tzv. konturnu integraciju koja se izučava u teoriji funkcija kompleksnih varijabli. Ono što ćemo ovde napomenuti jeste da ukoliko funkcija F(s) postoji, tada se inverzna Laplace-ova transformacija mora računati po pravoj σ=const. ta prava mora pripadati oblasti konvergencije funkcije F(s), što znači da oblast konvergencije mora biti takva da u njoj postoji pojas konačne čirine i beskonačne dužine: σ1 < Re{s} < σ2 .
Uopštem slučaju nalaženje inverzne Laplace-ove transformacije svodi se na primenu definicione formule, koja zahteva rešavanje integrala po kompleksnoj učestanosti, a što predstavlja tehnički složen matematički zadatak. Rešavanje ovog problema zahteva poznavanje kompleksne analize, a u osnovi se svodi na rešavanje integrala kompleksne varijable po zatvorenoj konturi ( rešavanje krivolinijskih integrala ). Međutim, kada se radi o primeni teorije linearnih signala i sistema u elektrotehnici, tj. njenim različitim oblastima, kao što su automatika, elektronika, energetika, telekomunikacije, teorija električnih kola, obrada signala, inverzna Laplace-ova transformacija svih tipičnih signala od interesa može se alternativno odrediti primenom metodologije razvoja kompleksnog lika signala na parcijalne razlomke, uz korišćenje tablice Laplace-ove transformacije i primenu odgovarajućih osobina Uopštem slučaju nalaženje inverzne Laplace-ove transformacije svodi se na primenu definicione formule, koja zahteva rešavanje integrala po kompleksnoj učestanosti, a što predstavljatehnički složen matematički zadatak. Rešavanjeovog problema zahteva poznavanje kompleksne analize, a u osnovi sesvodi na rešavanje integrala kompleksne varijable po zatvorenoj konturi( rešavanje krivolinijskih integrala ). Međutim, kada se radi o primeniteorije linearnih signala i sistema u elektrotehnici, tj. njenimrazličitim oblastima, kao što su automatika, elektronika, energetika,telekomunikacije, teorija električnih kola, obrada signala, inverznaLaplace-ova transformacija svih tipičnih signala od interesa može sealternativno odrediti metodologije razvoja kompleksnog lika signala naparcijalne razlomke, uz korišćenje tablice Laplaceove transformacijetipičnih parova i primenu odgovarajućih osobina Laplace-ovetransformacije.
Metod razvoja kompleksnog lika signala (Laplace-ove transformacije) na parcijalne razlomke može se primeniti samo kod signala f(t) čiji je kompleksni lik striktno racionalna funkcija, tj. predstavlja količnik dva polinoma sa realnim koeficijentima:
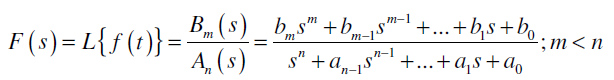
i takva da je red polinoma u brojiocu m striktno manji od reda n polinoma u imeniocu A(s), tj. m<n. Kod mnogih realnih signala i sistema, njihova Laplace-ova transformacija ima oblik striktno racionalne funkcije. Međutim, u realnim situacijama je takođe česta pojava kompleksnog lika koji predstavlja racionalnu funkciju, kod koje je m=n, a takav kompleksan lik se obično označava samo kao racionalna funkcija. U tom slučaju, da bi se primenila tehnika razvoja na parcijalne razlomke, prvo je potrebno da se podele polinomi i u brojiocu i u imeniocu, a rezultat takvog deljenja je određena konstanta, dok će ostatak deljenja omogućiti da se iz takve racionalne funkcije izdvoji striktno racionalan deo.
Koreni polinoma B(s) su nule, a koreni polinoma A(s) su polovi funkcije F(s). Za određivanje inverzne Laplace-ove transformacije su od posebnog značaja polovi funkcije F(s), i tu se mogu uočiti četiri karakteristična slučaja:
- Svi polovi funkcije F(s) su realni i prosti;
- Postoje konjugovano kompleksni polovi, a realni su, ako postoje, prosti;
- Funkcija F(s) ima višestruke realne korene;
- Funkcija F(s) ima višestruke konjugovano kompleksne polove.
Laplace-ove transformacije tipičnih signala
- Hevisajdov signal (jedinični odskočni signal)
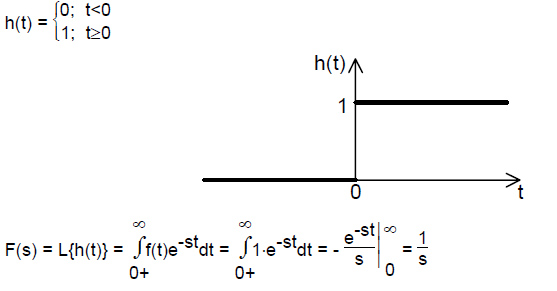
- Delta impuls (Dirakov impuls, jedinična impulsna funkcija).
Naovaj način se može opisati dejstvo sile pri idealnom udaru, gde je silabeskonačno velikog intenziteta a trajanja beskonačno malo (kratko). Poddejstvom ove sile se telu, ipak, dovodi konačna količina kretanja.
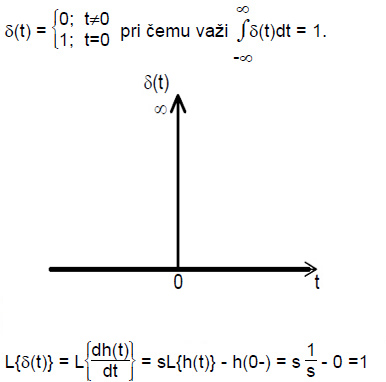
Deltaimpuls se može predstaviti kao izvod jediničnog odskočnog signala, pase pri određivanju LT primenjuje teorema o izvodu originala.
- Jedinični nagibni signal
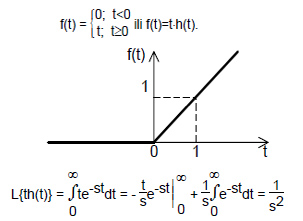
Polazni integral je rešen smenom: ∫udv=uv-∫vdu, gde je usvojeno: u=t, dv=e-stdt, odnosno du=dt i v= -1/s•e-st (parcijalna integracija).
Laplace-ova transformacija (nazvana po Pjer-Simon Laplasu ), iako je dobila ime u njegovu čast, jer je ovutransformaciju koristio u svom radu o teoriji verovatnoće, transformaciju je zapravo otkrio Leonard Ojler , švajcarski matematičar iz osamnaestog veka. Laplace-ova transformacija pojavljuje se u svim granama matematičke fizike – koja je bila glavno polje njegovih istraživanja. Laplasova diferencijalna oznaka, koja se često primenjuje u primenjenoj matematici, takođe je nazvana po njemu.
Literatura:
- Sistemi automatskog upravljanja, Katedre za automatiku i upravljanje procesima, FTN Novi Sad
- Signali i sistemi, Branko Kovačević, Željko Đurović, Srđan Stanković
- http://sr.wikipedia.org/sr-el/Laplasova_transformacija
Dalja objašnjenja pojmova korišćenih u ovom tekstu možete naći upomenutim knjigama.