Svaki sistem automatskog upravljanja se odlikuje određenim zakonom ili zakonima upravljanja. Zakon upravljanja predstavlja matematičku zavisnost na osnovu koje upravljački uređaj obrađuje relevantne signale i generiše odgovarajuća upravljačka dejstva. Najčešća forma ovakvih upravljačkih uređaja se naziva regulator.

Kod osnovnih zakona upravljanja njihovo dejstvo može linearno zavisiti od greške, njenog integrala ili prvog izvoda greške po vremenu. Na osnovu ove činjenice sledi podela regulatora na proporcionalni, integralni i diferencijalni regulator. Pomoću navedenih osnovnih regulatora moguće je formirati složenije oblike regulatora o kojima će biti više reči u nastavku teksta. Bez odzira na tip regulatora i način njegove realizacije, osnovni zahtevi za regulaciju sistema su: stabilnost, tačnost i brzina odziva.

Osnovni algoritam PID regulatora

 PID regulator ima tri podesiva parametra: pojačanje Kp, integralnu vremensku konstantu Ti i konstantu diferenciranja Td. Prisustvo proporcionalnog, integralnog i diferencijalnog dejstva u ovom regulatoru omugućuje dobijanje željenih performansi kao što su: stabilnost, brzina reagovanja, tačnost rada i vreme trajanja prelaznog procesa. Na slici br.1 možete videti blok šemu PID regulatora, na slici br.2 je prikazana jednačina koja opisuje upravljanje PID regulatora, dok je na slici br.3 je prikazano delovanje PID regulatora.

Slika br.1 Blok šema PID regulatora.
u(t)=K_p+K_i\int_0^te(t)dt+K_d\frac{de(t)}{dt}=K_p(e(t)+\frac{1}{T_i}\int_0^te(t)dt+T_d\frac{de(t)}{dt})
Slika br.2 Jednačina PID regulatora.
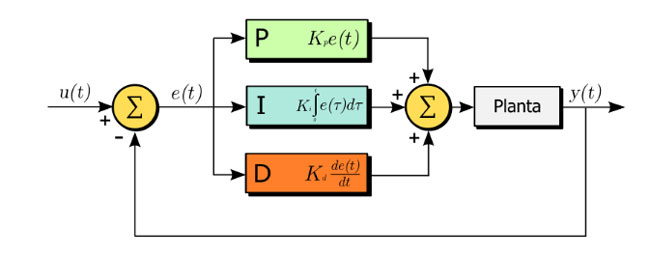
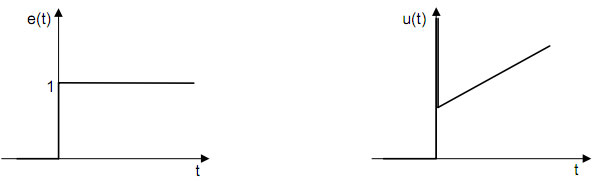
odziv pid_regulatora_automatika.rs

Slika br3. Delovanje PID regulatora.

Proporcionalno dejstvo (P regulator)

  P regulator predstavlja najjednostavniji tip regulatora koji se opisuje jednačinom:
u(t)=K_p*e(t)
gde Kp predstavlja faktor proporcionalnog dejstva ili pojačanje regulatora, a e(t) signal greške.
 Svaki proporcionalni regulator se odlikuje svojim proporcionalnim područjem koje se definiše kao potrebna procentualna promena ulazne veličine da bi se izlazna veličina promenila za 100%. Proporcionalno područje se može definisati i kao recipročna vrednost pojačanja Kp (%). Povećanjem pojačanja Kp, odnosno smanjenjem proporcionalnog područja, se konstantno odstupanje upravljane promenljive, od njene zadate vrednosti, smanjuje. U isto vreme se povećava brzina reagovanja i smanjuje pretek stabilnosti sistema. Na slici br.4 je prikazano delovanje P regulatora u(t) ako se na njegov ulaz dovodi signal greške e(t) u obliku jednačine odskočne funkcije.
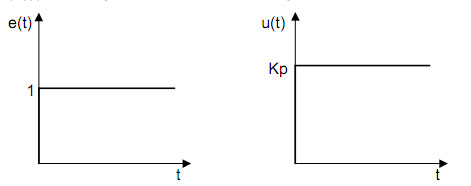
odziv p_regulatora_automatika.rs
Slika br.4 Delovanje P regulatora.

Integralno dejstvo (I regulator)

I regulator se opisuje jednačinom:
u(t)=K_i\int_0^te(t)dt

koja proporcionalno povezuje grešku e(t) sa brzinom promene upravljačke promenljive u(t). Recipročna vrednost pojačanja Ki je konstanta Ti i predstavlja vreme integralnog dejstva (vreme integraljenja).

K_i=\frac{1}{T_i}

Uvođenjem integralnog regulatora se povećava inertnost sistema, odnosno, sistem sporije  reaguje na spoljne uticaje, ali zato u većini slučajeva trajno otklanja grešku rada sistema u  stacionarnom stanju. Negativna osobina ovog tipa regulatora je i destabilizujuće dejstvo u sistemu usled njemu svojstvenog kašnjenja. Na slici br.5 je prikazano delovanje I regulatora, ako se na njegov ulaz dovodi signal greške e(t) u obliku jedinične odskočne  funkcije.

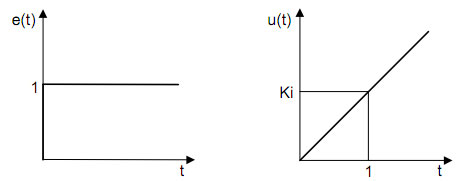
odziv i_regulatora_automati

Slika br.5 Delovanje I regulatora.


Diferencijalno dejstvo (D regulator)

D regulator opisuje jednačina:

u(t)=K_d\frac{de(t)}{dt}

Samostalno postojanje diferencijalnog regulatora nema mnogo smisla, jer je u ustaljenom režimu rada signal greške konstantan, te je izvod ovog signala jednak nuli. Zbog osobine da je promenljiva u(t) proporcionalna brzini promene (prvom izvodu) greške u vremenu vidi se da bi D regulator reagovao samo na brze promene dok spore i dugotrajne promene ne bi prouzrokovale nikakvo dejstvo ovog regulatora.

Kombinovanjem sa P i/ili I regulatorom, ovaj regulator dobija na značaju, posebno u prelaznom režimu rada sistema. Njegovo postojanje omogućava bolje praćenje dinamike sistema, jer se njime prati veličina promene greške, a ne samo njena apsolutna vrednost. Uvođenjem diferencijalnog regulatora se povećava stabilnost i brzina reagovanja sistema.

Proporcionalno-integralni regulator (PI regulator)

 Kombinacijom proporcionalnog i integralnog dejstva dobijamo PI regulator koji sadrži neke prednosti ovih dejstava. Upravljanje PI regulatorom opisano je sledećom jednačinom:

u(t)=K_pe(t)+K_i\int_0^te(t)dt

Ako se na ulazu PI regulatora pojavi signal u obliku odskočne funkcije proporcionalni član će trenutno postaviti izlaz u(t) na vrednost Kp, a pod uticajem integralnog  člana će u(t) nastaviti da raste linearno i u trenutku Ti će vrednost izlaza u(t) biti jednaka 2Kp. Na osnovu slike br.6 i jednačine PI regulatora se vidi da mora biti Ki*Ti=Kp, gde je Ti vremenska konstanta integracije. Drugim rečima, vreme integracije je vreme potrebno da se u(t) pod uticajem integralnog člana promeni za onu vrednost za koju se pod dejstvom proporcionalnog člana skokovito promenilo.

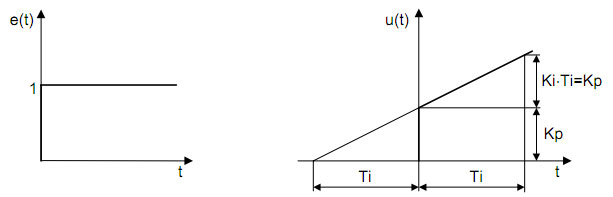odziv pi_regulatora_automatSlika br.6 Delovanje PI regulatora.
 Iz izraza za PI regulator se vidi da postoje dva podesiva parametra Kp i Ti. Pojačanje Kp u odsustvu integralnog dejstva predstavlja promenu u(t) za jediničnu promenu greške e(t). Podešavanje integralnog dejstva se vrši integralnom vremenskom konstantom Ti. U slučaju velikog proporcionalnog područja se pojavljuju spore oscilacije sa velikim amplitudama, a one su posledica smanjene brzine reagovanja usled integralnog dejstva.

Proporcijalno-diferencijalni regulator (PD regulator)


PD regulator je opisan sledećom jednačinom:

u(t)=K_pe(t)+K_d\frac{de(t)}{dt}

koja se može svesti na prikladniji oblik uvođenjem pojma derivacijskog vremena prema slici br.7.
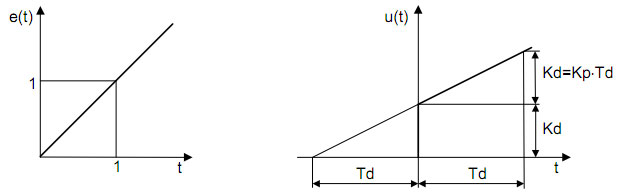
odziv pd_regulatora_automa
Slika br.7 Delovanje PD regulaora.

Pošto se radi o derivacijskom dejstvu pogodno je posmatrati poremećaj e(t) u obliku nagibne funkcije (neka bude jedinična nagibna funkcija radi jednostavnijeg objašnjenja). Ako se na ulaz PD regulatora dovodi nagibni signal tada treba da prođe vreme derivacije ili vremenska konstanta derivacije Td da bi se izlaz iz regulatora u(t) pod dejstvom proporcionalnog člana promenio za vrednost Kd za koju se u početku skokovito promenio pod dejstvom diferencijalnog člana. Drugim rečima, posle vremena Td vrednost upravljanja u(t) će biti 2Kd (a u trenutku t=0 je bilo u(t)=Kd), što daje vezu između Kp i Kd: Kd=KpTd ⇒ Kp=Kd/Td. Sada se predhodni izraz može napisati u obliku:

u(t)=K_p(e(t)+T_d\frac{de(t)}{dt})

 Pošto se PD upravljanje ne može definisati na osnovu odskočne promene greške e(t), jer je izvod odskočne funkcije u trenutku promene jednak beskonačnosti, onda se prema gore navedenom koristi linearna promena greške e(t)=E•t. Tada upravljački zakon PD regulatora ima oblik:

u(t)=K_p*E(t+T_d)

Iz ove jednačine se vidi da je za grešku e(t0)=E⋅t0 zadatu u trenutku t0, upravljačka promenljiva proporcionalna sa E•(t+Td), tj. sa greškom u trenutku (t+Td). Dakle, postoji efekat pomeranja upravljačkog signala unapred u vremenu za iznos Td, te se ova konstanta naziva još i konstanta prednjačenja. Prema tome, konstanta Td se definiše kao vremenski interval za koji diferencijalno dejstvo prednjači u vremenu, u odnosu na proporcionalno dejstvo, uz linearnu promenu greške.

Tekst je preuzet iz skripte prof. dr Dušana Petrovačkog za predmet Sistemi automatskog upravljanja. Dalja objašnjenja pojmova korišćenih u ovom tekstu možete naći u pomenutoj skripti.

POVEZANI ČLANCIVIŠE OD AUTORA

POSTAVI ODGOVOR

Please enter your comment!
Please enter your name here

This site uses Akismet to reduce spam. Learn how your comment data is processed.