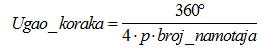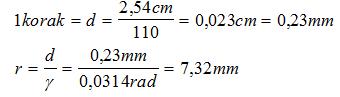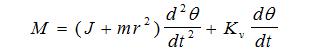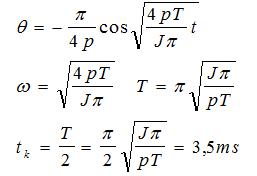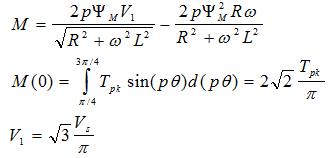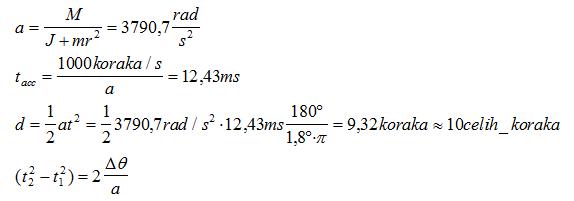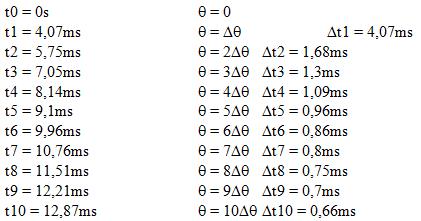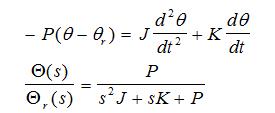Ovaj projektni rad je realizacija jednog pogona pisaće glave matričnog štampača izvedenog pomoću koračnog motora. Celim uređajem se upravlja pomoću računara koji je paralelnim kablom spojen sa uređajem. Sa računara se šalju komande tipa pomeri glavu za štampanje za n koraka u levo ili u desno ili pozicioniraj brzo glavu za štampanje na određenu poziciju.
Kratak opis korišćenog koračnog motora
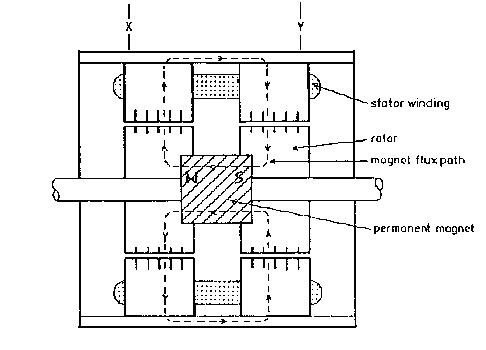
Korišćen je motor firme American Precision oznake 23D-6204. To je koračni motor hibridnog tipa, odnosno koračni motor sa stalnim magnetom. Ima bifilarno motane namotaje i to četiri namotaja. To omogućava dosta jednostavno elektronsko pogonsko kolo koje se sastoji od samo jednog tranzistora po namotaju. Brojni podaci o motoru navadeni su posle kratkog opisa rada takvog motora. Na sledećim slikama mogu se videti uzdužni i poprečni preseci jednog tipičnog koračnog motora sa stalnim magnetom.
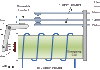
Slika 2. Uzdužni presek koračnog motora
Vidi se da ovakav motor ima stalni magnet postavljen duž osovine koji stavra stalni fluks kroz gvožđe mašine. I stator i rotor od magnetski mekog materijala – lameliranih limova imaju na svojim ivicama zubce kao što je prikazano na sledećoj slici (slika 2.).
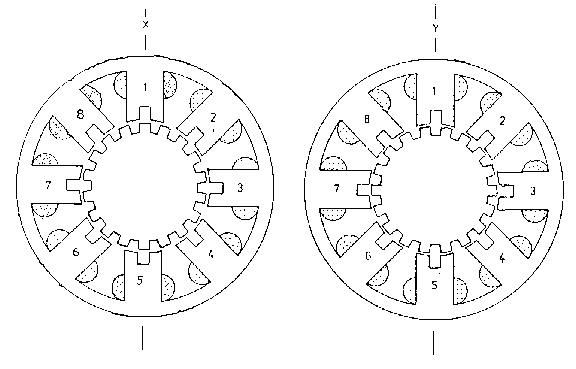
Slika 2. Poprečni presek koračnog motora
Na slici 1. se vidi da motor ima dva segmenta kako na rotoru, tako i na statoru. Poprečni presek ta dva segmenta je prikazan na slici 2. Pretpostavimo za početak da motor ima samo dva namotaja. Isti namotaj namotan je na zubcima obeleženim sa 1,5,3,7, a na preostalim zubcima drugi. Namotaji su motani tako da je fluks stvoren u zubcima 1 i 5 suprotnog znaka od onog u zubcima 3 i 7. Na isti način motan je i drugi namotaj samo što su kod njega parovi 2-6 i 4-8. Mali zupci na rotoru poklapaju se ili ne poklapaju sa malim zupcima na statoru. U slučaju pozitivne struje kroz prvi namotaj imamo najmanju reluktansu (magnetski otpor) kroz zupce 1-5 na Y segmentu i 3-7 na X segmentu. Fluks stalnog magneta biće vođen ovom putanjom. Samim tim sile koje će se javiti težiće da okrenu rotor baš u taj položaj da se mali zupci rotora i statora poklope baš kod zubaca 1-5Y i 3-7X. Ako sad želimo da motor načini korak, treba da prekinemo struju u prvom namotaju i da uključimo pozitivnu struju kroz drugi namotaj. Sada će najmanja reluktansa biti kroz zupce 2Y, 4X, 8X, 6Y. Zato će sila koja će se javiti težiti da okrene rotor u položaj takav da se poklope zupci statora i rotora upravo ispred ovih velikih zubaca. Sledeći koraci bi bili prekidanje struje kroz drugi namotaj i puštanje negativne struje kroz prvi namotaj, a zatim ukidanje te i puštanje negativne struje kroz drugi namotaj. Time je ciklus zavrešen i sledeće bi bilo ponovno puštanje pozitivne struje kroz prvi namotaj. Očigledno, broj malih zubaca rotora određuje veličinu koraka motora. Ovaj motor na slici ima mali broj zubaca pa mu je korak relativno velik. Obično je broj zubaca mnogo veći – i preko 50. Broj zubaca obeležava se obično sa p. Zavisnost ugla koraka, može se izračunati kao:
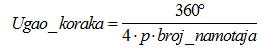
Nezgodno kod ovakvog motora je što zahteva i pozitivan i negativan smer struje kroz namotaje, što povlači komplikovaniju pogonsku elektroniku – bar četiri tranzistora po namotaju. Da bi se to izbeglo i da bi bio dovoljan i jedan tranzistor po namotaju, koristi se posebna verzija motora, a to je tzv. bifilarno motan koračni motor. Dva pomenuta namotaja se kod njega motaju sa dve niti, pa se dobiju četiri namotaja. Od njih su dva po dva identičnih karakteristika (istih induktivnosti i stvaraju poptpuno isti fuks). U kolo se vezuju tako da struja kroz njih iako uvek istog smera stvara suprotan fluks od njegovog para. Time se motor malo poskupljuje, ali pogonska elektronika se bitno pojeftinjuje.
Sada je jasno da treba obezbediti upravljanje koje će u ispravnom redosledu i u odgovarajućim vremenskim trenucima generisati upravljačke signale za uključivanje i isključivanje struja u namotajima čime će dovesti do ispravnog pozicioniranja tereta, u ovom slučaju pisaće glave matričnog štampača.
Pre navođenja osnovnih podataka o motoru, treba još objasniti neke stvari. Prvo, moment kojim motor teži da okrene rotor (naravno i vratilo sa teretom) zavisi od jačine struje kroz namotaje. Ta struja je ograničena mogućnostima disipacije toplote, i za svaki motor postoji tzv. procenjena vrednost struje faze (rated phase current). Fazom se naravno naziva namotaj. Moment u zavisnosti od ugla može da se aproksimira sinusoidom i navodi se u podacima kao vršna vrednost momenta pri propisanoj struji faze. Pošto motor sadrži stalni magnet, prisutan je izvestan fluks i kada motor uopšte nije pobuđivan. To je fiksirajući moment (detent torque) – može biti i koristan jer drži nepobuđivan motor u položaju, a inače je monogo manji od vršnog momenta. Naravno, tu su i induktivnosti namotaja i mehaničke konstante samog motora.
23D – 6204
- Otpor faznog namotaja 2.6 Ω;
- Procenjena jačina struje 1.8 A;
- Induktivnost faznog namotaja 5.7 mH;
- Vršni moment 0.5 Nm;
- Fiksirajući moment 0.0635 Nm;
- Inercija rotora 235g cm2
- Ugao koraka 1.80 ( p = 50)
Opis celokupne strukture sistema (mehaničke i električne)
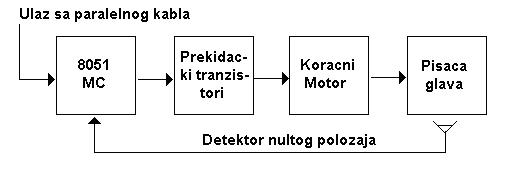
Ukratko, biće objašnjena struktura sistema kojim treba upravljati. Samo upravljanje vrši mikrokontroler (8051). On upravlja prekidačima koji uključiju i isključuju struju kroz pojedine namotaje koračnog motora (četvoronamotajnog, bifilarno motanog). Upravljanje motorom je u otvorenoj povratnoj sprezi. Možemo dozvoliti upravljanje u otvorenoj povratnoj sprezi jer se tačno zna korak motora, pa smim tim i pomeraj pisaće glave – opterećenja. A i karakteristike tog opterećenja su poznate, pa je i to razlog da upravljamo u otvorenoj povratnoj sprezi. To je i jednostavnije i jeftinije. Ipak, imamo jednu povratnu informaciju o tome gde se pisaća glava nalazi – detektujemo nulti položaj glave, a to je krajnje levi položaj. Ovo je neophodno da bismo posle reseta sistema mogli ponovo da postavimo glavu u inicijalni položaj i da bismo dalje mogli sa njom da upravljamo.
Glavu pomeramo pomoću zupčastog kaiša koji naleže na dva točkića na dva kraja hoda glave, a motor pogoni jedan od tih točkića. Sama glava nalazi se na nosaču koji se nalazi na točkićima sa jedne strane, a sa druge klizi po šipki koja prolazi kroz nosač, pružajući neko malo prigušenje pri pomeranju – viskozno trenje, koje je ipak poželjno pri ovakvoj primeni jer veoma je malo pa ne haba elemente preterano, a pruža ono malo prigušenja potrebnog za dovoljno brzo smirenje pisaće glave. Osim toga, njavećim delom za brzo smirenje prilikom pisanja, brine se posebno upravljanje tzv. hlaf stepping (upravljanje polovinom koraka), ali o tome kasnije.
Glavu pomeramo pomoću zupčastog kaiša koji naleže na dva točkića na dva kraja hoda glave, a motor pogoni jedan od tih točkića. Sama glava nalazi se na nosaču koji se nalazi na točkićima sa jedne strane, a sa druge klizi po šipki koja prolazi kroz nosač, pružajući neko malo prigušenje pri pomeranju – viskozno trenje, koje je ipak poželjno pri ovakvoj primeni jer veoma je malo pa ne haba elemente preterano, a pruža ono malo prigušenja potrebnog za dovoljno brzo smirenje pisaće glave. Osim toga, njavećim delom za brzo smirenje prilikom pisanja, brine se posebno upravljanje tzv. hlaf stepping (upravljanje polovinom koraka), ali o tome kasnije.
Evo i šematskog prikaza sistema:
Slika 3. Šematski prikaz sistema
Ovde je prikazana samo suštinska šema, detaljne električne šeme, a i nešto detaljniji opis mehaničkog dela, biće u drugom delu rada. Za sada samo jedan principski crtež samog pogonskog mehanizma:
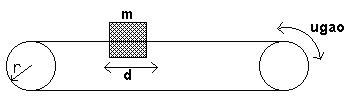
Slika3. Crtež pogonskog mehanizma
Ova slika biće neophodna za objašnjenje nekih izračunavanja u jednom od sledećih odeljaka.
Način upravljanja
Vreme je da se kaže nešto i o načinu upravljanja. Pre svega, mora da se objasni, kako se to upravlja ovim uređajem preko paralelnog kabla. Kako se upravlja samom pisaćom glavom, nije predmet ovog rada. O tehničkim detaljima komunikacije preko paralenog kabla, biće reči u drugom delu ovog rada. Za sada samo osnovno, koje se komande šalju ovom uređaju? Postoje dve vrste komandi. Jedna je komanda za pomeranje glave tako da se pri tome može pisati, dakle glave se svaki put pomeri, zaustavi i smiruje što je moguće brže, šalje se impuls preko kabla računaru da je glava pozicionirana i čeka se da računar drugim impulsom odgovori da je štampanje obavljeno i da kontroler može da pomeri glavu na sledeću poziciju. Komanda koja se šalje je komanda za koliko puta treba pomeriti pisaću glavu i na koju stranu.
Druga vrsa komandi služi za pozicioniranje glave na apsolutno zadatu poziciju i to što je moguće brže. Dakle motor se zaleće na oko 1500 koraka u sekundi, a zaustavlja se na tačno zadatoj poziciji. O formatu komandi u drugom delu. Ostaje još da se razmotri, kojim metodom upravljati motorom da se dobiju optimalne performanse rada za postizanje gore pomenutih zadataka. Prvo, da vidimo statičke momentne karakteristike koračnog motora:
Slika 4. Momentne statičke karakteristike koračnog motora
Ovo su naravno samo aproksimacije. Kod realnih motora karakteristike nešto odstupaju, ali u suštini svode se na sinusoudalni oblik. Periodične su kao i sinusoida, samo su nešto manje zaokrugljene. Analitički se mogu izraziti:
Ovde je TPK vršna vrednost momenta pri pobudi jedne faze. Nju predstavlja krajnje leva kriva. Druga kriva iste amplitude je zavisnost momenta od ugla pri pobuđivanju sledeće po redu faze. Ako pobuđujemo dve faze istovremeno, dobićemo karakteristiku između ove dve, a ona je za slučaj četvorofaznog bifilarnog koračnog motora:
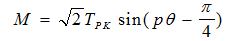
Vidimo da je nešto veće amlitude i pomerena je za pi/4 u desno. To možemo veoma korisno upotrebiti pri pomeranju glave za jedan položaj levo ili desno, i da pri tome dobijemo maksimalno prigušen odziv, ako vremenski pravilno uključujemo faze. Dakle, ako rotor miruje u ravnotežnom položaju (pi/4) pri uključenoj prvoj fazi. Sad uključimo i drugu ne gaseći prvu. Momentna karakteristika na tom mestu skače na najveći mogući moment i zaleće rotor napred. Zavisnost momenta od ugla je takva da bi rotor počeo da osciluje oko ravnotežnog položaja (pi/2), i to bi nastavio do beskonačnosti dok ga trenje ne bi zaustavilo. Međutim, ako mi u blizini suprotnog amplitudnog položaja (3pi/4) isključimo prvu fazu rotor se nalazi u blizini ravnotežne tačke za delovanje momenta pri uključenosti samo druge faze. Dakle već skoro zaustavljeni rotor biva doveden u blizinu sledećeg ravnotežnog položaja i odmah zatim i zaustavljen dejstvom momenta koji potiče samo od druge faze. Naravno, jasno je da je neophodna veoma precizna vremenska kontrola, ali mi raspolažemo sa dovoljno preciznim tajmerima na mikrokontroleru, pa ovo možemo primeniti. Naravno, ni karakteristike opterećenja se ne menjaju i poznate su, pa stoga ovakvo upravljanje možemo primeniti.
Ostaje još pitanje kako upravljati brzim pozicioniranjem. Suština je sledeća: nađe se zavisnost momenta od brzine obrtanja motora. Taj moment se naravno samnjuje kako brzina raste i ta se zavisnost može teorijski odrediti, o čemu će biti reči u narednom odeljku. Ostaje da se odredi u kojim vremenskim razmacima će morati da se menja pobuda da bi motor prvo ubrzao na željenu brzinu, zatim držao postignutu brzinu i konačno da bi počeo da usporava dovoljno koraka pred ciljem u kojem bi se tačno i zaustavio.
Naravno, pri svemu oveme, mora postojati i kontrola da li motor može da izvede zadati broj koraka jer je hod pisaće glave ograničen sa obe strane. Zatim, mora se predvideti i dovođenje glave u poznati nulti položaj prilikom reseta kao i stalna usputna kontrola svaki put kada se glava komanduje u nulti položaj, da li je zaista u njega i stigla. Sve ovo mora biti predviđeno algoritmom koji mikrokontroler izvršava. Naravno računar mora preko posebne linije biti obavešten i o tome ako je do neke greške u funkcionisanju došlo.
Ostaje još pitanje kako upravljati brzim pozicioniranjem. Suština je sledeća: nađe se zavisnost momenta od brzine obrtanja motora. Taj moment se naravno samnjuje kako brzina raste i ta se zavisnost može teorijski odrediti, o čemu će biti reči u narednom odeljku. Ostaje da se odredi u kojim vremenskim razmacima će morati da se menja pobuda da bi motor prvo ubrzao na željenu brzinu, zatim držao postignutu brzinu i konačno da bi počeo da usporava dovoljno koraka pred ciljem u kojem bi se tačno i zaustavio.
Naravno, pri svemu oveme, mora postojati i kontrola da li motor može da izvede zadati broj koraka jer je hod pisaće glave ograničen sa obe strane. Zatim, mora se predvideti i dovođenje glave u poznati nulti položaj prilikom reseta kao i stalna usputna kontrola svaki put kada se glava komanduje u nulti položaj, da li je zaista u njega i stigla. Sve ovo mora biti predviđeno algoritmom koji mikrokontroler izvršava. Naravno računar mora preko posebne linije biti obavešten i o tome ako je do neke greške u funkcionisanju došlo.
Izračunavanje svih parametara upravljanja
Da bi se moglo bilo šta dalje raditi, moraju se izračunati neke konkretne brojne vrednosti parametara električnog kola i brojne vremenske konstante za razne akcije. Nek to prvo bude vremenska konstanta električnog kola faze. Kako ovo kolo konkretno izgleda, može da se vidi na slikama na kraju drugog dela.
Kod bifilarno motanog koračnog motora, svaki namotaj ima osim sopstvene induktivnosti vrednosti L i međusobnu induktivnost sa svojim parom koji je sa njim bifilarno motan i vrednost te međuinduktivnosti iznosi M=L jer su oba namotaja po obliku skoro potpuno isti. Rešavanjem električnog kola može se utvrditi da je odziv struje na odskočnu pobudu sledećeg oblika:
Kod bifilarno motanog koračnog motora, svaki namotaj ima osim sopstvene induktivnosti vrednosti L i međusobnu induktivnost sa svojim parom koji je sa njim bifilarno motan i vrednost te međuinduktivnosti iznosi M=L jer su oba namotaja po obliku skoro potpuno isti. Rešavanjem električnog kola može se utvrditi da je odziv struje na odskočnu pobudu sledećeg oblika:
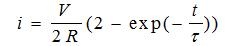
gde je R ukupna otpornost kola – dalke otpornost namotaja i tzv. prisilne otpornosti koja ima ulogu da smanji vremensku konstantu tau, V napon jednosmernog napajanja, a tau=2L/R vremenska konstanta. Za dvofazni ne-bifilarno motani motor ta konstanta je dva puta manja. Ako se uzme V=26V kao sasvim prihvatljiva, tada pošto je procenjena vrednost struje I=1,8A, otpornost mora biti R=14.6oma, dakle spoljašnja prisilna otpornost mora biti Rf=12oma. Maksimalna disipacija na tom otporniku biće P = I2R = 38,9W. Mora biti u stanju da disipira toliku snagu. Vremenska konstanta u tom slučaju iznosi 0,95ms, što sasvim odgovara, budući da u sporom radu očekivana brzina pomeranja iznosi do 200-300 koraka u sekundi maksimalno, a trajanje tih koraka nadmašuje ovu vremensku konstantu i do deset puta.
Sledeće je da se odrede vremenske konstante pri režimu sporog koračanja. Za početak, mora se odrediti dimenzija točkića u pogonu pisaće glave. Poznato je da nam je potrbna rezolucija štampanja od 110dpi odnosno tačaka po inču. Prost račun pokazuje da je potreban pomeraj d, imamo motor sa uglom koraka od 1,8 stepeni, ostaje da se odredi r, tj. poluprečnik točkića.
Sledeće je da se odrede vremenske konstante pri režimu sporog koračanja. Za početak, mora se odrediti dimenzija točkića u pogonu pisaće glave. Poznato je da nam je potrbna rezolucija štampanja od 110dpi odnosno tačaka po inču. Prost račun pokazuje da je potreban pomeraj d, imamo motor sa uglom koraka od 1,8 stepeni, ostaje da se odredi r, tj. poluprečnik točkića.
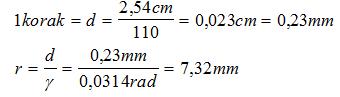
jer je 1.8 stepeni = 0.0314radijana. Kada smo to rešili jasno je da motor mora da obrće teret inercije.
gde je J moment inercije rotora koji je zadat, a drugi član je doprinos tereta – glave za štampanje mase m.
Sad, kad su poznati mehanički parametri motora i opterećenja, može se napisati diferencijalna jednačina kretanja rotora (uključeno je i optrećenje). Dakle:
Sad, kad su poznati mehanički parametri motora i opterećenja, može se napisati diferencijalna jednačina kretanja rotora (uključeno je i optrećenje). Dakle:
M je naravno moment koji deluje na rotor i biće o njemu reči podrobnije. Kv je koeficient trenja koji doprinosi prigušenju oscilacija. U ovom momentu on nije toliko bitan pa će biti samtran nulom.
Za M će biti korišćena aproksimacija, i to linearna. Grafički, biće prikazana na sledećoj slici. Prava koja povezuje vršne vrednosti sinusoide pri pobudi samo jedne faze biće aproksimacija za slučaj kada je uključena samo jedna faza, a prava koja povezuje tačke na sinusoidi pri pobudi sa dve uključene faza u dve susedne ravnotežne tačke pri pobudi sa samo jednom uključenom fazom aproksimiraće moment pri dve faze uključene.
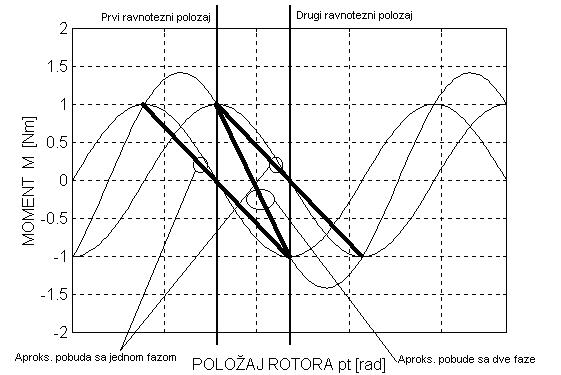
Za M će biti korišćena aproksimacija, i to linearna. Grafički, biće prikazana na sledećoj slici. Prava koja povezuje vršne vrednosti sinusoide pri pobudi samo jedne faze biće aproksimacija za slučaj kada je uključena samo jedna faza, a prava koja povezuje tačke na sinusoidi pri pobudi sa dve uključene faza u dve susedne ravnotežne tačke pri pobudi sa samo jednom uključenom fazom aproksimiraće moment pri dve faze uključene.
Slika 5.
Odavde se mogu izvesti analitički izrazi za momente.
T je naravno vršni moment. Levi M je u slučaju pobude jednom fazom, a desni u slučaju pobude sa dve. Pretpostavimo da se rotor nalazi u ravnotežnom položaju i miruje. Tada uključimo i drugu fazu i počinje da važi moment za dve faze. Dakle ako rešimo gornju diferencijalnu jednačinu za ovaj moment, zanemarimo prigušenje, treba da izračunamo trenutak kada rotor stiže u suprotnu amplitudnu tačku, odnosno u novi ravnotežni položaj. To je trenutak kada treba da isključimo prvu fazu. Rešenje diferencijalne jednačine za taj slučaj glasi:
tk je naravno ta polovina periode, odnosno vreme uključenosti druge faze. Time je određeno sve za realizaciju ove funkcije. Ostaje nam samo analiza brzog hoda motora.
Šta je osnovni porblem ovde? Od motora se zahtevaju brzine na koje se on ne može ubrzati za vreme jednog koraka. Prema tome, kada bi se jednostavno uključila pobuda koja je te zahtevane frekvencije, motor bi krenuo, ali bi odmah počeo i da zaostaje za pobudom, sve dok se ne bi zaleteo i neizvesno je šta bi se desilo, ali krajnji rezultat bi sigurno bio pogrešno pozicioniranje zbog izgubljenih koraka. Slično važi i za zaustavljanje. Drugo, ni momoent motora nije jedanak pri svakoj brzini. Osnovni razlog leži u tome što fazni namotaji imaju konačne vremenske konstante, pa pri brzoj promeni pobude u njima jednostavno ne stiže da se uspostavi procenjena vrednost struje. Osim toga, rotor koji se okreće stvara ems u namotajima koji se oduzima od faznog napona, pa struja i ne može da poraste do vršne vrednosti. Uzimajući sve ovo u obzir može se uz određene aproksimacije i idealizacije izvesti formula koja daje ovu zavisnost momenta od brzine. Ona glasi:
Šta je osnovni porblem ovde? Od motora se zahtevaju brzine na koje se on ne može ubrzati za vreme jednog koraka. Prema tome, kada bi se jednostavno uključila pobuda koja je te zahtevane frekvencije, motor bi krenuo, ali bi odmah počeo i da zaostaje za pobudom, sve dok se ne bi zaleteo i neizvesno je šta bi se desilo, ali krajnji rezultat bi sigurno bio pogrešno pozicioniranje zbog izgubljenih koraka. Slično važi i za zaustavljanje. Drugo, ni momoent motora nije jedanak pri svakoj brzini. Osnovni razlog leži u tome što fazni namotaji imaju konačne vremenske konstante, pa pri brzoj promeni pobude u njima jednostavno ne stiže da se uspostavi procenjena vrednost struje. Osim toga, rotor koji se okreće stvara ems u namotajima koji se oduzima od faznog napona, pa struja i ne može da poraste do vršne vrednosti. Uzimajući sve ovo u obzir može se uz određene aproksimacije i idealizacije izvesti formula koja daje ovu zavisnost momenta od brzine. Ona glasi:
M(0) je moment izračunat sa statičke karakteristike uz pretpostavku da je maksimalni moment u tom slučaju jednak srednjoj vresnosti gornje ovojnice statičkih karakteristika pojedinih faza redom uključivanih. On nam je neophodan za nalaženje PsiM. V1 je amplituda prvog harmonika pobudnog napona jedne faze. Na osnovu svega toga, dobija se PsiM=0,0046Wb (fluks), a za V=26V : V1=14.33V. Prema toj formuli, nacrtan je grafik:
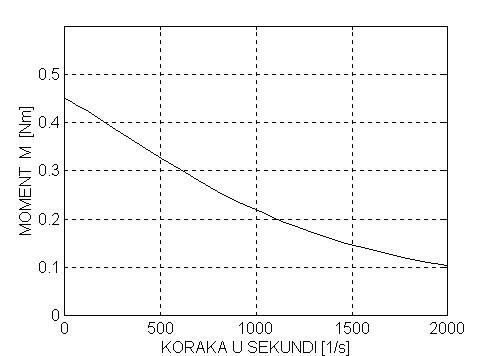
Slika 6.
Pri brzini za koju smo zainteresovani (1500) koraka, imamo moment od oko 0,15Nm. Ostaje da se odrede vremena promene pobude pri zaletanju motora, a ista se vremena u obrnutom redosledu mogu koristiti za usporavanje motora pred ciljem.
Radi jednostavnosti, smatraćemo da motor ubrzava upravo pogonjen najmanjim momentom od 0,15Nm. Tako sigurno nećemo pogrešiti jer je moment tokom ubrzavanja sigurno i veći. Ako samtramo da je moment stalan, tada i motor ubrzava konstantnim ubrzanjem – a, koje ćemo prvo izračunati. Naći ćemo odmah zatim i vreme potrebno za ubrzavanje na zahtevanu brzinu. Znajući to vreme, možemo odrediti broj koraka potrebnih za ubrzavanje. Evo svih potrebnih proračuna:
Radi jednostavnosti, smatraćemo da motor ubrzava upravo pogonjen najmanjim momentom od 0,15Nm. Tako sigurno nećemo pogrešiti jer je moment tokom ubrzavanja sigurno i veći. Ako samtramo da je moment stalan, tada i motor ubrzava konstantnim ubrzanjem – a, koje ćemo prvo izračunati. Naći ćemo odmah zatim i vreme potrebno za ubrzavanje na zahtevanu brzinu. Znajući to vreme, možemo odrediti broj koraka potrebnih za ubrzavanje. Evo svih potrebnih proračuna:
Vremena do petog koraka su sledeć, računajući prema poslednjoj formuli:
Dalje se nastavlja sa tim vremenom jer je to upravo interval izme]u koraka pri brzini od 1500koraka/s, odnosno Deltat = 1/1500 = 0,0066ms = 2/3ms. To se nastavlja sve do 10 koraka pred ciljem. Jedanaesti korak pred ciljem mora da traje 4/3ms jer se kočenje mora započeti. Ono se započinje na sledeći način: ne menja se pobuda za vreme od dva koraka, a pušta se da motor radi po istoj momentnoj karakteristici – karakteristici tog koraka. Tako se zađe u negativni deo momentne karakteristike gde moment zapravo koči rotor umesto da ga ubrzava. Za usporenje se jednostavno ponovi ova ista sekvenca ali u suprotnom smeru. Tu nešto pomaže i trenje ali to u ovoj analizi nije uzeto u obzir.
Eto, to bi bili svi parametri pogona i upravljanja. Ostaje da se pojedini momenti provere u simulaciji. Na osnovu svega rečenog, može se napraviti upravljački uređaj.
Modelovanje sistema
Precizno modelovanje koračnog motora nije nimalo jednostavan zadatak. Reč je o objektu koji zbog svoje strukture i načina rada zahteva model koji je pun nelinearnih elemenata. Njime se upravlja preko prekidačkih elemenata, prema tome struktura kola se pri tome menja. Za upravljanje ne koristi se jedna ili više jednosmernih ili prostoreriodičnih veličina što umnogome otežava ako ne i onemogućava izgradnju jednostavnog linearnog modela. Ovde je uz izvesne pretpostavke upotrebljen jedan linearni model koji bi trebalo da bude u stanju da da upotrebljive rezultate, barem za slučajeve koji se pojavljuju u ovom radu.
Pretpostavlja se da je pogonski moment motora linearna funkcija ugla rotora stim što se nulta vrednost te funkcije šeta u zavisnosti od toga koji je namotaj pobuđivan i u kom položaju se nalazi rotor. Drugim rečima, prava koja predstavlja ovaj linearizovani moment šeta se duž uglovne ose u zavisnosti od pobude. Ostalo je jasno, imamo sistem sa jednim stepenom slobode, rotor momenta inercije jednakog sopstvenom momentu inercije i momentu inercije koji se dodaje zbog opterećenja. Osim toga, mora se uzeti i odgovarajući koeficient viskoznog trenja koji je uvek prisutan i doprinosi prigušenju oscilacija. Dakle, diferencijalna jednačina svega rečenog i prenosna funkcija koja se na osnovu nje dobija su sledeće (prenosna funkcija od položaja preseka momenta sa uglovnom osom koji zavisi od trenutne pobude i položaja rotora, o kome će biti vođeno računa prilikom simulacije, do ugla položaja rotora):
Pretpostavlja se da je pogonski moment motora linearna funkcija ugla rotora stim što se nulta vrednost te funkcije šeta u zavisnosti od toga koji je namotaj pobuđivan i u kom položaju se nalazi rotor. Drugim rečima, prava koja predstavlja ovaj linearizovani moment šeta se duž uglovne ose u zavisnosti od pobude. Ostalo je jasno, imamo sistem sa jednim stepenom slobode, rotor momenta inercije jednakog sopstvenom momentu inercije i momentu inercije koji se dodaje zbog opterećenja. Osim toga, mora se uzeti i odgovarajući koeficient viskoznog trenja koji je uvek prisutan i doprinosi prigušenju oscilacija. Dakle, diferencijalna jednačina svega rečenog i prenosna funkcija koja se na osnovu nje dobija su sledeće (prenosna funkcija od položaja preseka momenta sa uglovnom osom koji zavisi od trenutne pobude i položaja rotora, o kome će biti vođeno računa prilikom simulacije, do ugla položaja rotora):
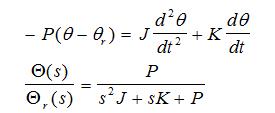
P je vršni moment za neki uglovni položaj odnosno pobudu. J je već pominjani moment inercije, a K je koeficient viskoznog trenja. Kao što je već i ranije korišćeno J=395,7*10-7kgm2. P se menja u zavisnosti od mnogo čega, pa će svuda biti naglašeno koliko je. Za K će biti uzeto 531,9*10-6kgm2/s. K se može odrediti eksperimentalno recimo na osnovu toga što će se teret u posmatranom sistemu ubrzati na neku brzinu, naravno sve pogonske sile su isključene, i posmatraće se vreme za koje se teret zaustavi. Pet puta manje vreme od tog možemo smatrati vremenskom konstantom sistema (u toj konkretnoj situaciji ispitivanja samo). Tad je Tau=J/K. Kako je sve poznato, lako se nalazi K. Sad su spremni svi elementi da bi moglo da se pređe na simulaciju.
Simulacija rada
Prvo bi trebalo pogledati, kako se sistem odaziva na promenu pobude, kada se rotor nalazi u ravnotežnom položaju, a onda se uključi i naredna faza i stvori se moment koji pokreće rotor na odgovarajuću stranu. Naravno očekuje se oscilatoran odziv što je i uzeto u obzir pri primenjenom upravljanju sporim pomeranjem pisaće glave. Dakle prvo dve faze da se rotor pokrene, pa u suprotnom amplitudnom položaju, samo se isključi prethodna faza. Novi moment samo blago povlači rotor u novi položaj skoro bez ikakvih oscilacija. P je u ovom slučaju 4pT/ što odgovara pobuđivanju sa dve faze. prvo skače na 0,9 što je polovina koraka, a nakon dostizanja suprotne amplitude na 1,8. Na simulacionom diagramu, to se postiže sabiranjem dva odskočna signala. Simulacioni diagram je sledeći:
Slika 7. Simulacioni dijagram
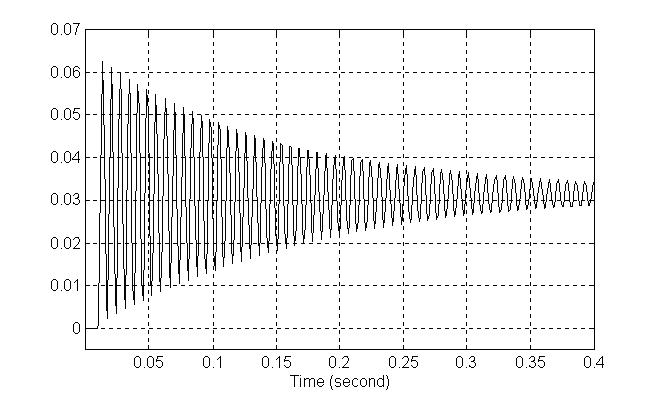
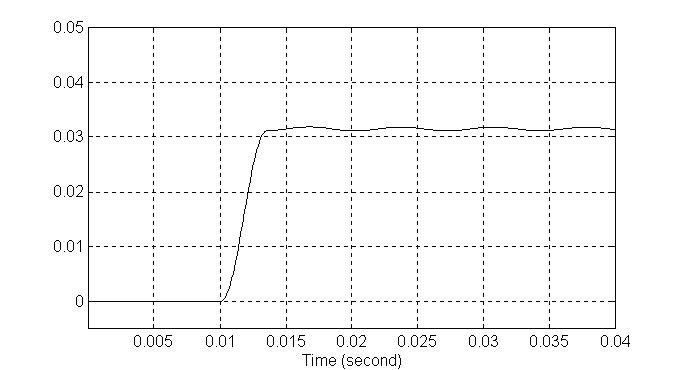
Za početak, odziv sistema prilikom uključivanja sledeće faze, da bi se videla perioda oscilacija i momenat dostizanja pomentuog položaja. Promena faza nastupa u trenutku 0,01s. Vidi dobar deo odziva i stepen oscilatornosti, mada je u realnom slučaju prigušenje i znatno veće.
Slika 8.
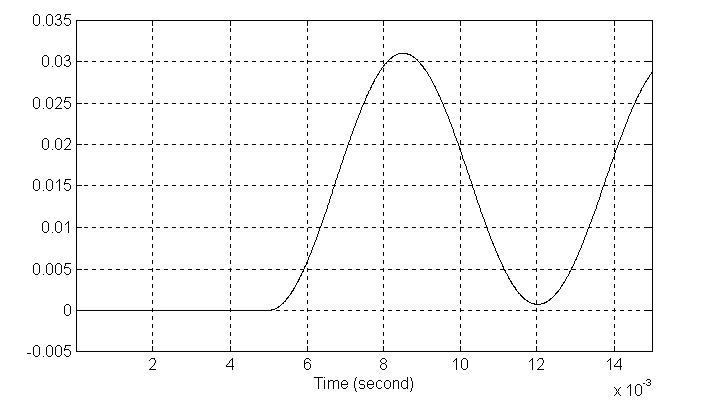
Na drugoj slici, vidi se jedan odziv na identičnu pobudu koja nastupa u trenutku t=0.005s. Ovde je deo od interesa veoma uvećan i vidi se tačno pominjana tačka u kojoj će biti potrebno promeniti pobudu da bi se rotor doveo u novi položaj sa minimalnim oscilacijama. Vidi se da je proračun bio dosta tačan i da se zaista radi o trenutku 3,5ms nakon uključivanja druge faze.
Slika 9.
Na sledećoj slici prikazana je simulacija odziva kada se 3,5ms nakon uključivanja druge faze isključi prva. Odziv je skoro idealan. Postoje neka blaga talasanja, ali pisaća glava je već nakon 5-6ms spremna da otkuca nešto jer su oscilacije zanemarljive amplitude.
Slika 10.
Vidi se, da pobuda počinje u trenutku 0,01s, a već u trenutku 0,015s teret je pozicioniran i dovoljno miran za upotrebu. To bi bilo sve što se tiče ovog režima rada. Na redu je brzo pozicioniranje.
Ovaj režim se simulira uz upotrebu istog modela. Kao ulaz dolazi stepeničasta funkcija koja ima skokove na svim mestima kada treba sa se desi promena pobude. Svaki put se tada uveća za ugao jednog koraka. Skokovi su sve češći kako se rotor ubrzava kroz deset koraka, zatim se drži konstantna brzina kroz nekoliko koraka nakon čega počinje usporavanje – prvo jedan korak dvostruke dužine, a zatim obrnuta sekvenca usporavanja sve dok se motor ne zaustavi na 26. koraku kako nalaže i pobuda koja je u ovom slučaju veoma slična grafiku ugla – kao neki referentni signal. Na slikama su date redom izgled simulaciono diagrama, grafik pozicije ugla rotora, grafik pobude – refernetnog signala i konačno grafik brzine koja se nalazi kao izvod ugla položaja rotora.
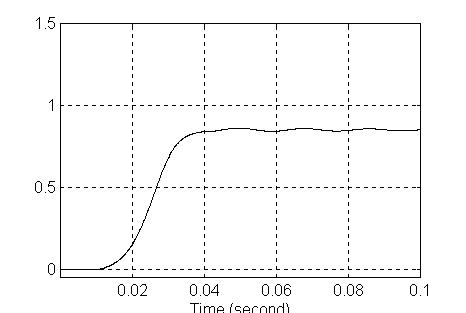
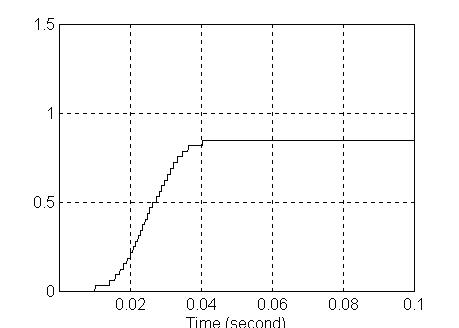
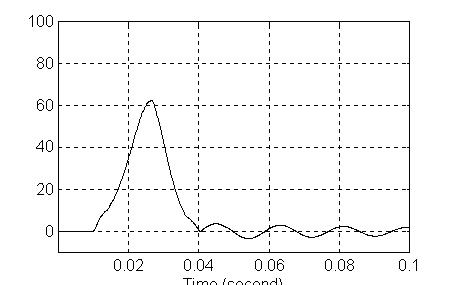
Ovaj režim se simulira uz upotrebu istog modela. Kao ulaz dolazi stepeničasta funkcija koja ima skokove na svim mestima kada treba sa se desi promena pobude. Svaki put se tada uveća za ugao jednog koraka. Skokovi su sve češći kako se rotor ubrzava kroz deset koraka, zatim se drži konstantna brzina kroz nekoliko koraka nakon čega počinje usporavanje – prvo jedan korak dvostruke dužine, a zatim obrnuta sekvenca usporavanja sve dok se motor ne zaustavi na 26. koraku kako nalaže i pobuda koja je u ovom slučaju veoma slična grafiku ugla – kao neki referentni signal. Na slikama su date redom izgled simulaciono diagrama, grafik pozicije ugla rotora, grafik pobude – refernetnog signala i konačno grafik brzine koja se nalazi kao izvod ugla položaja rotora.
Slika 11.
Slika 12.
Slika13.
Slika 14.
Vidimo da je ubrzavanje uspešno kao i usporavanje. Prisutne se manje oscilacije nakon dostizanja krajneg ravnotežnog položaja. Uzrok tome je ipak delimično aproksimativno određivanje šeme za ubrzavanje kao i usporavanje. Nakon uspešnog dostizanja cilja posle brzog pozicioniranja, teret se smiruje i spreman je za dalja pojedinačna spora pomeranja ili na neko novo brzo pozicioniranje.
Zaključak
U ovom radu urađeno je teorijsko razmatranje upravljanja koračnim motorom uz pomoć mikrokontrolera u otvorenoj povratnoj sprezi. Na početku objašnjena je struktura koračnog motora uopšte, a odmah zatim i sistem za pozicioniranje pisaće glave štampača i položaj koračnog motora u svemu tome.
Zatim je objašnjena suština načina upravljanja tim motorom u oba režima rada upravljačkog uređaja. Date su i obrazložene sve jednačine na osnovu kojih se dolazi do ključnih parametara sistema nakon čega su oni i izračunati.
Dat je i jedan veoma jednostavan ali efikasan metod za modelovanje koračnog motora, doduše samo njegovog mehaničkog dela, ali parametri koji su pod uticajem električnog dela detaljno su proučeni u prethodnim delovima. Zatim su dati i simulcaioni diagrami svih režima kao i rezultati simulacija.
Sudeći po rezultatima simulacija, ponašanje tako upravljanog sistema odgovara zahtevima koji se postavljaju pred jedan ovakav upravljački uređaj: dovoljno brzo smirivanje posle jednog koraka pri sporom koračnom pomeranju i precizno i brzo pozicioniranje u režimu brzog pozicioniranja.
Doduše, sistem ima i izvesnih nedostataka kao što su upadljive oscilacije nakon pozicioniranja, ali to bi se moglo rešiti uz upotrebu upravljanja u povratnoj sprezi što bi bilo mnogo skuplje i složenije rešenje. Jednostavan lek za taj problem mogao bi da bude pokušaj da se taj poslednji korak načini uz pomoć jednog polukoraka kao što se to čini u režimu pojedinačnih pomeranja.
Još nešto mora da se pomene, a to je da na početku pominjani fiksirajući moment nije uziman u obzir tokom analiza jer bi usložnio analize, a mnogo je manji od pogonskog momenta tako da veoma malo i utiče na krajnje rezultate.
Zatim je objašnjena suština načina upravljanja tim motorom u oba režima rada upravljačkog uređaja. Date su i obrazložene sve jednačine na osnovu kojih se dolazi do ključnih parametara sistema nakon čega su oni i izračunati.
Dat je i jedan veoma jednostavan ali efikasan metod za modelovanje koračnog motora, doduše samo njegovog mehaničkog dela, ali parametri koji su pod uticajem električnog dela detaljno su proučeni u prethodnim delovima. Zatim su dati i simulcaioni diagrami svih režima kao i rezultati simulacija.
Sudeći po rezultatima simulacija, ponašanje tako upravljanog sistema odgovara zahtevima koji se postavljaju pred jedan ovakav upravljački uređaj: dovoljno brzo smirivanje posle jednog koraka pri sporom koračnom pomeranju i precizno i brzo pozicioniranje u režimu brzog pozicioniranja.
Doduše, sistem ima i izvesnih nedostataka kao što su upadljive oscilacije nakon pozicioniranja, ali to bi se moglo rešiti uz upotrebu upravljanja u povratnoj sprezi što bi bilo mnogo skuplje i složenije rešenje. Jednostavan lek za taj problem mogao bi da bude pokušaj da se taj poslednji korak načini uz pomoć jednog polukoraka kao što se to čini u režimu pojedinačnih pomeranja.
Još nešto mora da se pomene, a to je da na početku pominjani fiksirajući moment nije uziman u obzir tokom analiza jer bi usložnio analize, a mnogo je manji od pogonskog momenta tako da veoma malo i utiče na krajnje rezultate.
