Kirhofove zakone predstavljaju dve jednačine koje opisuju odnos struje i napona u električnim kolima. Prvi ih je opisao Gustaf Kirhof, u 19.veku, a one su nastale daljim izvođenjem Omovog zakona. Imaju široku primenu u elektrotehnici i nazivaju se Kirhofovim pravilima ili Kirhofovi zakonima.
Prvi Kirhofov zakon
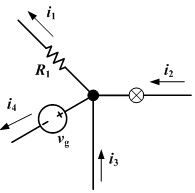
Prvi Kirhofov zakon naziva se još i Kirhofov strujni zakon i glasi: zbir struja koje ulaze u čvor je jednak zbiru struja koje izlaze iz tog čvora.
Kada imamo stalno strujno polje raspored električnih naelektrisanja u prostoru je vremenski nepromenljiv a na mesto pokretnih naelektrisanja koja napuste svoje mesto dolazi ista količina novih pokretnih naelektrisanja. Količina naelektrisanja koja se uđe u čvor mora da bude jednaka količini koja za isto vreme otekne iz čvora.
Zakon kontinuiteta za naelektrisanje glasi:
Q1+Q4=Q2+Q3
Ako ovu jednačinu relaciju podelimo sa vremenom t dobijamo sledeće:
I1+I4 = I2 + I3
Jednačina koja opisuje Prvi Kirhofov zakon glasi:
\sum\limits_{k=1}^n Ik=0
Napomena: Prvi Kirhofov zakon je važeći samo ukoliko je ukupno naelektrisanje Q konstantno u razmatranom opsegu.
Drugi Kirhofov zakon
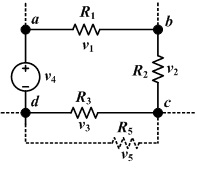 Drugi Kirhofov zakon naziva se još i Kirhofov naponski zakon i glasi: suma svih napona u konturi je jednaka nuli.
Drugi Kirhofov zakon naziva se još i Kirhofov naponski zakon i glasi: suma svih napona u konturi je jednaka nuli.
V1 +V2 +V3 + V4 = 0
U svakoj konturi električnog kola zbir napona na svim otporima jednak je zbiru svih elektromotornih sila u toj konturi. Ovo postaje jasnije kada se sagleda da je polaritet napona na otporima suprotan polaritetu izvora napona, pa zbir daje nulu.
Jednačina koja opisuje Drugi Kirhofov zakon glasi:
\sum\limits_{k=1}^n Vk=0
Ovaj zakon se zasniva na jednom od Maksvelovih jednačina (Maksvel – Faradejev zakon indukcije) u kome se navodi da je pad napona oko jedne zatvorene konture jednak stopi promene fluksa koji seče tu konturu. Vrednsot fluksa zavisi od zahvaćene oblasti konture i jačine magnetnog polja. Drugi kirhofov zakon kaže da je vrednost napona te konture jednaka nuli.
Napomena: Drugi Kirhofov zakon se zasniva na pretpostavci da ne postoji promenljivo magnetno polje koje utiče na zatvorenu konturu, što nije primenljivo na naizmenična kola.




















![iCUB nominovan da nosi baklju na ovogodišnjim Olimpijskim igrama u Londonu [VIDEO]](https://www.automatika.rs/wp-content/uploads/2012/07/sddefault-1-218x150.jpg)