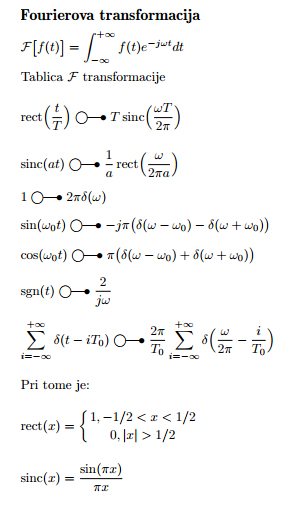Još u 19. veku su postavljeni osnovi tehnike za transformaciju signala u frekvencijski domen, i ona je našla primenu u gotovo svim oblastima nauke i tehnike. Vrlo često se neki složeni problemi u vremenskom domenu veoma jednostavno rešavaju analizom u frekvencijskom domenu.
Frekvencijski domen sadrži sve informacije koje sadrži i vremenski, samo su one predstavljene u drugom obliku. Signal je u frekvencijskom domenu opisan svojim amplitudskim i faznim spektrom, koji predstavljaju promenu amplitude i faze u zavisnosti od frekvencije.
Opšti termin Fourier-ova analiza se odnosi na:
- Fourier-ov red (kontinualni periodični signali)
- Fourier-ovu transformaciju (kontinualni neperiodični signali)
- Fourier-ovu transformaciju diskretnih signala DTFT (diskretni signali)
- Diskretnu Fourier-ovu transformaciju DFT (nastaje diskretizacijom jedne periode Fourierove transformacije)
Fourier-ova analiza se zasniva na dekompoziciji signala na sumu više sinusnih signala. Sinusni signali su pogodniji za obradu od nekog složenog signala. Ukoliko se na ulaz linearnog vremenski invarijantnog sistema dovede sinusni signal, signal na izlazu mora takođe biti sinusni signal iste frekvencije, a sistem na njega može uticati samo kroz promenu amplitude i faze. Sinusni signali su jedini koji imaju to svojstvo.
Joseph Fourier je započeo proučavanje Fourier-ovih redova kako bi rešio toplotnu jednačinu. Jean Baptiste Joseph Fourier (21.mart 1768. – 16.maj 1830.godine) je bio francuski matematičar i fizičar, najpoznatiji po iniciranju istraživanja Fourier-ovih redova i njihove primene na probleme prenosa toplote. Fourier-ova transformacija je, takođe, dobila naziv u njegovu čast.
Fourier-ov red
Neka je dat kontinualni signal x(t) koji je periodičan sa periodom T. On se može predstaviti kao suma sinusoidalnih signala čije su ugaone frekvencije celobrojni umnošci osnovne ugaone frekvencije Ω0 = 2π/T. Na ovaj način se signal predstavlja u obliku Fourier-ovog reda, odnosno u obliku:
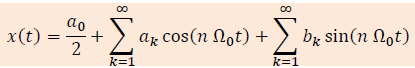
Koeficijenti Fourier-ovog reda su određeni izrazima:
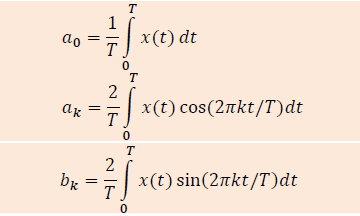
Ukoliko je signal x(t) parna funkcija, svi koeficijenti biće jednaki nuli. Ukoliko je signal neparna funkcija, važiće a0=ak=0, a za k=1:N .
Fourier-ova transformacija
S obzirom na primenljivost Fourier-ovih redova u analizi periodičnih signala, bilo je vrlo važno razviti tehniku koja se može primenjivati i na neperiodične signale. Neperiodični signal se može posmatrati kao periodični signal sa beskonačno velikom periodom.
Mogu se izvesti dve izuzetno važne relacije koje definišu takozvanu Fourier-ovu transformaciju:
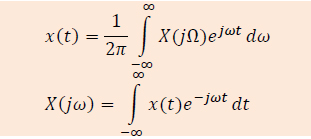
Dakle, navedene relacije se primenjuju na neperiodične kontinualne signale. Signal x(t) i funkcija X(jω) nazivaju se Fourier-ov transformacioni par.
Fourier-ov transformat X(jω) je kompleksan broj, i iz njega se dobijaju oba spektra:
![]()
Na slici ispod je prikazana tablica Fourirer-ovih transformacija